【题目】已知函数.

（1）讨论函数的单调性；

（2）若直线与曲线的交点的横坐标为，且，求整数所有可能的值.

在平面直角坐标系中，直线的参数方程为（为参数， 为倾斜角），以坐标原点O为极点， 轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为

（1）求曲线的直角坐标方程，并 求C的焦点F的直角坐标；

（2）已知点，若直线与C相交于A,B两点，且，求的面积.

【题目】甲、乙两人玩转盘游戏，该游戏规则是这样的：一个质地均匀的标有12等分数字格的转盘（如图），甲、乙两人各转转盘一次，转盘停止时指针所指的数字为该人的得分．（假设指针不能指向分界线）现甲先转，乙后转，求下列事件发生的概率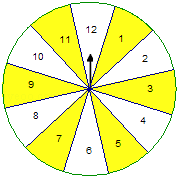

（1）甲得分超过7分的概率．
（2）甲得7分，且乙得10分的概率
（3）甲得5分且获胜的概率．

【题目】已知函数f（x）是（﹣∞，0）∪（0，+∞）上的奇函数，且当x＜0时，函数的部分图象如图所示，则不等式xf（x）＜0的解集是（ ）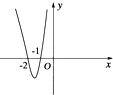

A.（﹣2，﹣1）∪（1，2）
B.（﹣2，﹣1）∪（0，1）∪（2，+∞）
C.（﹣∞，﹣2）∪（﹣1，0）∪（1，2）
D.（﹣∞，﹣2）∪（﹣1，0）∪（0，1）∪（2，+∞）

【题目】小王创建了一个由他和甲、乙、丙共4人组成的微信群，并向该群发红包，每次发红包的个数为1个（小王自己不抢），假设甲、乙、丙3人每次抢得红包的概率相同．
（Ⅰ）若小王发2次红包，求甲恰有1次抢得红包的概率；
（Ⅱ）若小王发3次红包，其中第1，2次，每次发5元的红包，第3次发10元的红包，记乙抢得所有红包的钱数之和为X，求X的分布列和数学期望．

【题目】已知函数f（x）=ax2﹣2ax+b（a＞0）在区间[﹣1，4]上有最大值10和最小值1．设g（x）= ．
（1）求a、b的值；
（2）证明：函数g（x）在[ ，+∞）上是增函数；
（3）若不等式g（2x）﹣k2x≥0在x∈[﹣1，1]上有解，求实数k的取值范围．

已知函数

（1）求不等式的解集；

（2）若，求证： .

根据以上数据，技术人员分别借助甲、乙两种不同的回归模型，得到了两个回归方程，甲：

为了评价两种模型的拟合效果，完成以下任务：

（1）（ⅰ）完成下表（计算结果精确到0.1）：

（ⅱ）分别计算模型甲与模型乙的残差平方和及，并通过比较,的大小，判断哪个模型拟合效果更好.

（2）该书上市后，受到广大读者的热烈欢迎，不久便全部售罄，于是印刷厂决定进行二次印刷，根据市场调查，新需求量为8千册（概率为0.8）或10千册（概率为0.2），若印刷厂以没测5元的价格将书籍出售给订货商，问印刷厂二次印刷8千册还是10千册恒获得更多的利润？（按（1）中拟合效果较好的模型计算印刷单册书的成本）

【题目】某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A，B，C三家社区医院，并且他们的选择是相互独立的．
（Ⅰ）求甲、乙两人都选择A社区医院的概率；
（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；
（Ⅲ）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望．

【题目】我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强，几乎达到100%，据监测：服药后每毫升血液中的含药量y（微克）与时间r（小时）之间近似满足如图所示的曲线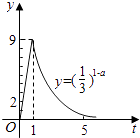

（1）写出第一服药后y与t之间的函数关系式y=f（x）；
（2）据进一步测定：每毫升血液中含药量不少于 微克时，治疗有效，求服药一次后治疗有效的时间是多长？