【题目】若x，y满足约束条件 ，且向量 =（3，2）， =（x，y），则 的取值范围（ ）
A.[ ，5]
B.[ ，5]
C.[ ，4]
D.[ ，4]

【题目】已知函数， .

（1）若，求曲线在点处的切线方程；

（2）讨论函数的单调性.

【题目】如图，地面上有一竖直放置的圆形标志物，圆心为C，与地面的接触点为G．与圆形标志物在同一平面内的地面上点P处有一个观测点，且PG=50m．在观测点正前方10m处（即PD=10m）有一个高为10m（即ED=10m）的广告牌遮住了视线，因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧．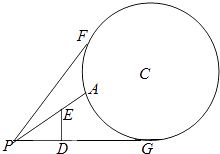

（1）若圆形标志物半径为25m，以PG所在直线为x轴，G为坐标原点，建立直角坐标系，求圆C和直线PF的方程；
（2）若在点P处观测该圆形标志的最大视角（即∠APF）的正切值为 ，求该圆形标志物的半径．

【题目】在R上定义运算：xy=x（1﹣y），若不等式（x﹣a）（x﹣b）＞0的解集是（2，3），则a+b的值为（ ）
A.1
B.2
C.4
D.8

（1）某高校某专业要求选考科目物理，考生若要报考该校该专业，则有多少种选考科目的选择；

（2）甲、乙、丙三名同学都选择了物理、化学、历史组合，各学科成绩达到二级的概率都是0.8，且三人约定如果达到二级不参加第二次考试，达不到二级参加第二次考试，如果设甲、乙、丙参加第二次考试的总次数为，求的分布列和数学期望．

【题目】如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC点，F棱AC上，且AF=3FC．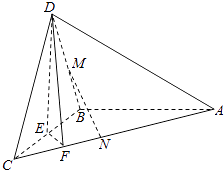

（1）求三棱锥D﹣ABC的体积；
（2）求证：AC⊥平面DEF；
（3）若M为DB中点，N在棱AC上，且CN= CA，求证：MN∥平面DEF．

【题目】已知椭圆： 的左焦点和上顶点在直线上， 为椭圆上位于轴上方的一点且轴， 为椭圆上不同于的两点，且．

（1）求椭圆的标准方程；

（2）设直线与轴交于点，求实数的取值范围．

【题目】已知集合A={x|y= }，B={x|log2x≤1}，则A∩B=（ ）
A.{x|﹣3≤x≤1}
B.{x|0＜x≤1}
C.{x|﹣3≤x≤2}
D.{x|x≤2}

【题目】如图，在四棱柱为长方体，点是上的一点.

（1）若为的中点，当为何值时，平面平面；

（2）若， ，当时，直线与平面所成角的正弦值是否存在最大值？若存在，求出的值；若不存在，请说明理由.

【题目】已知数列{bn}满足bn=3bn﹣1+2（n≥2），b1=1．数列{an}的前n项和为Sn ， 满足Sn=4an+2
（1）求证：{bn+1}是等比数列并求出数列{bn}的通项公式；
（2）求数列{an}的通项公式和前n项和公式．