
科目: 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了50名女性和50名男性,根据调研结果得到如图所示的等高条形图
(1)完成下列2×2列联表:
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关” 附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)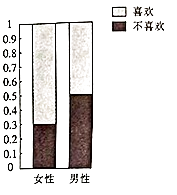
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为 ![]() 的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则
的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则 ![]() =
=
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0 , 2 ![]() )(x0>
)(x0> ![]() )是抛物线C上一点,圆M与线段MF相交于点A,且被直线x=
)是抛物线C上一点,圆M与线段MF相交于点A,且被直线x= ![]() 截得的弦长为
截得的弦长为 ![]() |MA|,若
|MA|,若 ![]() =2,则|AF|等于( )
=2,则|AF|等于( )
A.![]()
B.1
C.2
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的方程为:
的方程为: ![]() 。
。
(1)求圆![]() 的圆心所在直线方程一般式;
的圆心所在直线方程一般式;
(2)若直线![]() 被圆
被圆![]() 截得弦长为
截得弦长为![]() ,试求实数
,试求实数![]() 的值;
的值;
(3)已知定点![]() ,且点
,且点![]() 是圆
是圆![]() 上两动点,当
上两动点,当![]() 可取得最大值为
可取得最大值为![]() 时,求满足条件的实数
时,求满足条件的实数![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务,某市移动公司欲提供新的资费套餐(资费包含手机月租费、手机拨打电话费与家庭宽带上网费)。其中一组套餐变更如下:
原方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
18元/月 | 0.2元/分钟 | 50元/月 |
新方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
58元/月 | 前100分钟免费, 超过部分 | 免费 |
(1)客户甲(只有一个手机号和一个家庭宽带上网号)欲从原方案改成新方案,设其每月手机通话时间为![]() 分钟(
分钟(![]() ),费用
),费用![]() 原方案每月资费-新方案每月资费,写出
原方案每月资费-新方案每月资费,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)经过统计,移动公司发现,选这组套餐的客户平均月通话时间![]() 分钟,为能起到降费作用,求
分钟,为能起到降费作用,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
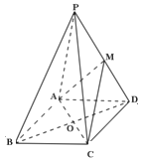
【题目】如图,已知在正四棱锥![]() 中,
中, ![]() 为侧棱
为侧棱![]() 的中点, 连接
的中点, 连接![]() 相交于点
相交于点![]() 。
。
(1)证明: ![]() ;
;
(2)证明: ![]() ;
;
(3)设![]() ,若质点从点
,若质点从点![]() 沿平面
沿平面![]() 与平面
与平面![]() 的表 面运动到点
的表 面运动到点![]() 的最短路径恰好经过点
的最短路径恰好经过点![]() ,求正四棱锥
,求正四棱锥 ![]() 的体积。
的体积。
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读与探究
人教A版《普通高中课程标准实验教科书 数学4(必修)》在第一章的小结中写到:
将角放在直角坐标系中讨论不但使角的表示有了统一的方法,而且使我们能够借助直角坐标系中的单位圆,建立角的变化与单位圆上点的变化之间的对应关系,从而用单位圆上点的纵坐标、横坐标来表示圆心角的正弦函数、余弦函数.因此,正弦函数、余弦函数的基本性质与圆的几何性质(主要是对称性)之间存在着非常紧密的联系.例如,和单位圆相关的“勾股定理”与同角三角函数的基本关系有内在的一致性;单位圆周长为![]() 与正弦函数、余弦函数的周期为
与正弦函数、余弦函数的周期为![]() 是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.
是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.

依据上述材料,利用正切线可以讨论研究得出正切函数![]() 的性质.
的性质.
比如:由图1.2-7可知,角![]() 的终边落在四个象限时均存在正切线;角
的终边落在四个象限时均存在正切线;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线缩为一个点,值为
轴上时,其正切线缩为一个点,值为![]() ;角
;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线不存在;所以正切函数
轴上时,其正切线不存在;所以正切函数![]() 的定义域是
的定义域是![]() .
.
(1)请利用单位圆中的正切线研究得出正切函数![]() 的单调性和奇偶性;
的单调性和奇偶性;
(2)根据阅读材料中途1.2-7,若角![]() 为锐角,求证:
为锐角,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中![]() 小时以内(含
小时以内(含![]() 小时)每张球台
小时)每张球台![]() 元,超过
元,超过![]() 小时的部分每张球台每小时
小时的部分每张球台每小时![]() 元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于
元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于![]() 小时,也不超过
小时,也不超过![]() 小时,设在甲家租一张球台开展活动
小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)试分别写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com