【题目】已知方程.

（Ⅰ）若此方程表示圆，求的取值范围；

（Ⅱ)若（Ⅰ）中的圆与直线相交于， 两点，且（为坐标原点），求；

（Ⅲ）在（Ⅱ)的条件下，求以为直径的圆的方程.

【题目】已知在 的展开式中，第6项为常数项．
（Ⅰ）求含x2的项的系数；
（Ⅱ）求展开式中所有的有理项．

【题目】某城市上年度电价为0.80元/千瓦时，年用电量为千瓦时.本年度计划将电价降到0.55元/千瓦时～0.7元/千瓦时之间，而居民用户期望电价为0.40元/千瓦时（该市电力成本价为0.30元/千瓦时)，经测算，下调电价后，该城市新增用电量与实际电价和用户期望电价之差成反比，比例系数为.试问当地电价最低为多少元/千瓦时，可保证电力部门的收益比上年度至少增加20%.

【题目】已知函数，若

（1）求的值，并写出函数的最小正周期（不需证明）；

（2）是否存在正整数，使得函数在区间内恰有个零点？若存在，求出的值；若不存在，请说明理由.

【题目】在三棱柱ABC﹣A1B1C1中，侧面ABB1A1为矩形，AB=2，AA1=2 ，D是AA1的中点，BD与AB1交于点O，且CO⊥平面ABB1A1 ．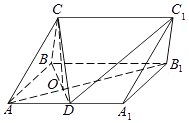

（1）证明：CD⊥AB1；
（2）若OC=OA，求直线CD与平面ABC所成角的正弦值．

【题目】已知函数（为常函数）是奇函数.

（1）判断函数在上的单调性，并用定义法证明你的结论；

（2）若对于区间上的任意值，使得不等式恒成立，求实数的取值范围.

【题目】已知函数.

（1）求函数的定义域；

（2）判断的奇偶性；

（3）方程是否有实根？如果有实根，请求出一个长度为的区间，使；如果没有，请说明理由（注：区间的长度）

【题目】在直角坐标系中，圆与轴相切于点，且圆心在直线上.

(Ⅰ)求圆的标准方程；

(II)设为圆上的两个动点， ,若直线和的斜率之积为定值2，试探求的最小值．

【题目】某公司为了研究年宣传费（单位：千元）对销售量（单位：吨）和年利润（单位：千元）的影响，搜集了近 8 年的年宣传费和年销售量数据：

(Ⅰ)请补齐表格中 8 组数据的散点图，并判断与中哪一个更适宜作为年销售量关于年宣传费的函数表达式？（给出判断即可，不必说明理由）

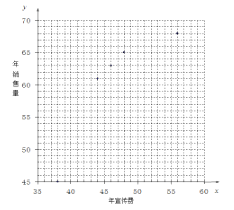
(Ⅱ)若(Ⅰ)中的，且产品的年利润与， 的关系为，为使年利润值最大，投入的年宣传费 x 应为何值？

【题目】如图，在直四棱柱中，底面是梯形， .

(Ⅰ)求证： ；

(Ⅱ)若,点为线段的中点．请在线段上找一点,使平面，并说明理由.