
科目: 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)设Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设f(x)=. ![]() ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】化简
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)切化弦可得三角函数式的值为-1
(2)结合三角函数的性质可得三角函数式的值为![]()
试题解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(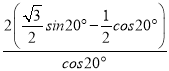 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
点睛:三角函数式的化简要遵循“三看”原则:一看角,这是重要一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式 ;二看函数名称,看函数名称之间的差异,从而确定使用的公式,常见的有切化弦;三看结构特征,分析结构特征,可以帮助我们找到变形的方向,如遇到分式要通分等.
【题型】解答题
【结束】
18
【题目】平面内给定三个向量![]()
(1)求![]()
(2)求满足![]() 的实数
的实数![]() .
.
(3)若![]() ,求实数
,求实数![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).

【答案】①②
【解析】试题分析:①:如图,当![]() 时,
时, ![]() 与
与![]() 相交于点
相交于点![]() ,∵
,∵![]() ,则
,则![]() ,
,
∴![]() ,∴①正确;②:由于对称性,
,∴①正确;②:由于对称性, ![]() 恰好是正方形的面积,
恰好是正方形的面积,
∴![]() ,∴②正确;③:显然
,∴②正确;③:显然![]() 是增函数,∴
是增函数,∴![]() ,∴③错误.
,∴③错误.

考点:函数性质的运用.
【题型】填空题
【结束】
17
【题目】化简
(1)![]()
(2)![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,a∈R.
(1)当x=1时,函数f(x)取得极值,求a的值;
(2)当0<a< ![]() 时,求函数f(x)在区间[1,2]上的最大值;
时,求函数f(x)在区间[1,2]上的最大值;
(3)当a=﹣1时,关于x的方程2mf(x)=x2(m>0)有唯一实数解,求实数m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】锐角△ABC中,角A、B、C所对的边分别为a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB).
(1+tanAtanB).
(Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
【答案】(1) 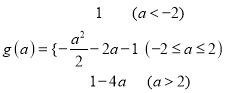 ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用同角三角函数间的基本关系化简函数解析式后,分三种情况:①![]() 小于﹣1时②
小于﹣1时②![]() 大于﹣1而小于1时③
大于﹣1而小于1时③![]() 大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把
大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把![]() 代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
试题解析:
(1)由![]()
![]() .这里
.这里![]()
①若![]() 则当
则当![]() 时,
时, ![]()
②若![]() 当
当![]() 时,
时, ![]()
③若![]() 则当
则当![]() 时,
时, ![]()
因此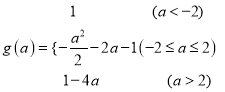
(2)![]()
![]() ①若
①若![]() ,则有
,则有![]() 得
得![]() ,矛盾;
,矛盾;
②若![]() ,则有
,则有![]() 即
即![]() 或
或![]() (舍).
(舍).
![]()
![]() 时,
时, ![]() 此时
此时![]()
当![]() 时,
时, ![]() 取得最大值为5.
取得最大值为5.
点睛:二次函数在闭区间上必有最大值和最小值,它只能在区间的端点或二次函数图象的顶点处取到;常见题型有:(1)轴固定区间也固定;(2)轴动(轴含参数),区间固定;(3)轴固定,区间动(区间含参数). 找最值的关键是:(1)图象的开口方向;(2)对称轴与区间的位置关系;(3)结合图象及单调性确定函数最值.
【题型】填空题
【结束】
21
【题目】已知两个不共线的向量![]() 的夹角为
的夹角为![]() ,且
,且![]() 为正实数.
为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() ;
;
(2)若![]() ,求
,求![]() 的最小值及对应的
的最小值及对应的![]() 的值,并指出此时向量
的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数
为锐角,对于正实数![]() ,关于
,关于![]() 的方程
的方程![]() 有两个不同的正实数解,且
有两个不同的正实数解,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com