
科目: 来源: 题型:
【题目】已知 ![]() ,函数
,函数 ![]() .
.
(1)当 ![]() 时,解不等式
时,解不等式 ![]() ;
;
(2)若关于 ![]() 的方程
的方程 ![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求 ![]() 的取值范围;
的取值范围;
(3)设 ![]() ,若对任意
,若对任意 ![]() ,函数
,函数 ![]() 在区间
在区间 ![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某游艇制造厂研发了一种新游艇,今年前5个月的产量如下:

(1)设![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() 现根据表中数据已经正确计算出了
现根据表中数据已经正确计算出了![]() 的值为
的值为![]() ,试求
,试求![]() 的值,并估计该厂
的值,并估计该厂![]() 月份的产量;(计算结果精确到
月份的产量;(计算结果精确到![]() )
)
(Ⅱ)质检部门发现该厂![]() 月份生产的游艇都存在质量问题,要求厂家召回;现有一旅游公司曾向该厂购买了今年前两个月生产的游艇
月份生产的游艇都存在质量问题,要求厂家召回;现有一旅游公司曾向该厂购买了今年前两个月生产的游艇![]() 艘,求该旅游公司有游艇被召回的概率.
艘,求该旅游公司有游艇被召回的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
查看答案和解析>>
科目: 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目: 来源: 题型:
【题目】某班级50名学生的考试分数x分布在区间[50,100)内,设分数x的分布频率是f(x)且f(x)= 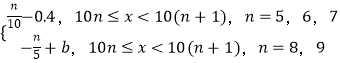 ,考试成绩采用“5分制”,规定:考试分数在[50,60)内的成绩记为1分,考试分数在[60,70)内的成绩记为2分,考试分数在[70,80)内的成绩记为3分,考试分数在[80,90)内的成绩记为4分,考试分数在[90,100)内的成绩记为5分.用分层抽样的方法,现在从成绩在1分,2分及3分的人中用分层抽样随机抽出6人,再从这6人中抽出3人,记这3人的成绩之和为ξ(将频率视为概率).
,考试成绩采用“5分制”,规定:考试分数在[50,60)内的成绩记为1分,考试分数在[60,70)内的成绩记为2分,考试分数在[70,80)内的成绩记为3分,考试分数在[80,90)内的成绩记为4分,考试分数在[90,100)内的成绩记为5分.用分层抽样的方法,现在从成绩在1分,2分及3分的人中用分层抽样随机抽出6人,再从这6人中抽出3人,记这3人的成绩之和为ξ(将频率视为概率).
(1)求b的值,并估计班级的考试平均分数;
(2)求P(ξ=7);
(3)求ξ的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 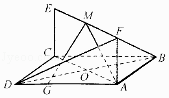
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com