
科目: 来源: 题型:
【题目】“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注“微信运动”公众号查看自己及好友每日行走的步数、排行榜,也可以与其他用户进行运动量的![]() 或点赞.现从某用户的“微信运动”朋友圈中随机选取40人,记录他们某一天的行走步数,并将数据整理如下:
或点赞.现从某用户的“微信运动”朋友圈中随机选取40人,记录他们某一天的行走步数,并将数据整理如下:
步数/步 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | 10000以上 |
男性人数/人 | 1 | 6 | 9 | 5 | 4 |
女性人数/人 | 0 | 3 | 6 | 4 | 2 |
规定:用户一天行走的步数超过8000步时为“运动型”,否则为“懈怠型”.
(1)将这40人中“运动型”用户的频率看作随机抽取1人为“运动型”用户的概率.从该用户的“微信运动”朋友圈中随机抽取4人,记![]() 为“运动型”用户的人数,求
为“运动型”用户的人数,求![]() 和
和![]() 的数学期望;
的数学期望;
(2)现从这40人中选定8人(男性5人,女性3人),其中男性中“运动型”有3人,“懈怠型”有2人,女性中“运动型”有2人,“懈怠型”有1人.从这8人中任意选取男性3人、女性2人,记选到“运动型”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一款手机,每部购买费用是5000元,每年网络费和电话费共需1000元;每部手机第一年不需维修,第二年维修费用为100元,以后每一年的维修费用均比上一年增加100元.设该款手机每部使用![]() 年共需维修费用
年共需维修费用![]() 元,总费用
元,总费用![]() 元.(总费用
元.(总费用![]() 购买费用
购买费用![]() 网络费和电话费
网络费和电话费![]() 维修费用)
维修费用)
(1)求函数![]() 、
、![]() 的表达式:
的表达式:
(2)这款手机每部使用多少年时,它的年平均费用最少?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着共享单车的蓬勃发展,越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况,某共享单车公司对某区域不同年龄的骑乘者进行了调查,得到数据如下:
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
(1)求![]() 关于
关于![]() 的线性回归方程,并估计年龄为40岁人群的骑乘人数;
的线性回归方程,并估计年龄为40岁人群的骑乘人数;
(2)为了回馈广大骑乘者,该公司在五一当天通过![]() 向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是![]() ,
,![]() ,
,![]() ,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为
,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为正整数,集合
为正整数,集合![]() (
(![]() ),对于集合
),对于集合![]() 中的任意元素
中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(1)当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,设
时,设![]() 是
是![]() 的子集,且满足:对于
的子集,且满足:对于![]() 中的任意元素
中的任意元素![]() 、
、![]() ,当
,当![]() 、
、![]() 相同时,
相同时,![]() 是奇数,当
是奇数,当![]() 、
、![]() 不同时,
不同时,![]() 是偶数,求集合
是偶数,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】食品安全一直是人们关心和重视的问题,学校的食品安全更是社会关注的焦点.某中学为了加强食品安全教育,随机询问了36名不同性别的中学生在购买食品时是否看保质期,得到如下“性别”与“是否看保质期”的列联表:
男 | 女 | 总计 | |
看保质期 | 8 | 22 | |
不看保持期 | 4 | 14 | |
总计 |
(1)请将列联表填写完整,并根据所填的列联表判断,能否有![]() 的把握认为“性别”与“是否看保质期”有关?
的把握认为“性别”与“是否看保质期”有关?
(2)从被询问的14名不看保质期的中学生中,随机抽取3名,求抽到女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,(
,(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为6的正方形![]() 中,弧
中,弧![]() 的圆心为
的圆心为![]() ,过弧
,过弧![]() 上的点
上的点![]() 作弧
作弧![]() 的切线,与
的切线,与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 边于点
边于点![]() .
.
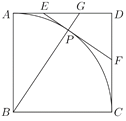
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出函数定义域;
之间的函数解析式,并写出函数定义域;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com