
科目: 来源: 题型:
【题目】数列{an}的前n项和记为Sn且满足Sn=2an﹣1,n∈N*;
(1)求数列{an}的通项公式;
(2)设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n+1anan+1 , 求{Tn}的通项公式;
(3)设有m项的数列{bn}是连续的正整数数列,并且满足:lg2+lg(1+ ![]() )+lg(1+
)+lg(1+ ![]() )+…+lg(1+
)+…+lg(1+ ![]() )=lg(log2am).
)=lg(log2am).
问数列{bn}最多有几项?并求出这些项的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分16分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由;
的范围(或值),若不存在,请说明理由;
(3)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a( ![]() ),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计)
),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计) 
(1)如图(2)所示,FH和GE的延长线交于点O,求证:OE=40cot ![]() (cm);
(cm);
(2)当a= ![]() π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
查看答案和解析>>
科目: 来源: 题型:
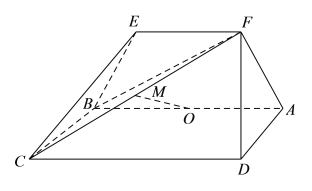
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,矩形
的中点,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直.
互相垂直.
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )设
)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(![]() )求三棱锥
)求三棱锥![]() 的体积.(只写出结果,不要求计算过程)
的体积.(只写出结果,不要求计算过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是函数![]() 的导函数
的导函数![]() 的图象,给出下列命题:
的图象,给出下列命题:
①-2是函数![]() 的极值点;
的极值点;
②1是函数![]() 的极值点;
的极值点;
③![]() 的图象在
的图象在![]() 处切线的斜率小于零;
处切线的斜率小于零;
④函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
则正确命题的序号是( )

A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.函数
单调递增.函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间;(只写结论,不需证明)
的单调区间;(只写结论,不需证明)
(2)求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)讨论方程![]() 实根的个数.
实根的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知 f(x)= ![]() sin2x﹣2sin2x,
sin2x﹣2sin2x,
(1)求f(x)的最小正周期和单调递减区间;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值及取得最大值时对应的x的取值.
],求f(x)的最大值及取得最大值时对应的x的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com