
科目: 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1=2,且a2+1,a4+1,a8+1成等比数列.
(1)求数列{an}通项公式;
(2)设数列{bn}满足bn= ![]() ,求适合方程b1b2+b2b3+…+bnbn+1=
,求适合方程b1b2+b2b3+…+bnbn+1= ![]() 的正整数n的值.
的正整数n的值.
查看答案和解析>>
科目: 来源: 题型:
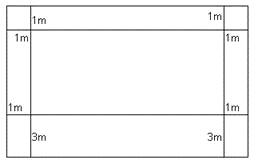
【题目】某村计划建造一个室内面积为800平米的矩形蔬菜温室,在温室内沿左右两侧与后墙内侧各保留1米的通道,沿前侧内墙保留3米宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大的种植面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为![]() ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为![]() ,
,![]() (
(![]() >
>![]() ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
|
|
|
|
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求![]() ,
,![]() 的值;
的值;
(Ⅲ)求数学期望![]() ξ。
ξ。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
(Ⅰ)求证:AB⊥DE;
(Ⅱ)求直线EC与平面ABE所成角的正弦值;
(Ⅲ)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出 ![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一个巨大的汽油灌,已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击相互独立,且命中概率都是![]() ,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为
,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校高三年级有学生1000名,经调查,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分两层)从该年级的学生中抽查100名同学.如果以身高达到165厘米作为达标的标准,对抽取的100名学生进行统计,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
积极参加体育锻炼 | 40 | ||
不积极参加体育锻炼 | 15 | ||
总计 | 100 |
(1)完成上表;
(2)能否有犯错率不超过0.05的前提下认为体育锻炼与身高达标有关系?(![]() 的观测值精确到0.001).
的观测值精确到0.001).
参考公式:![]() ,
,
参考数据:
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元。
(1)设铁栅长为![]() 米,一堵砖墙长为
米,一堵砖墙长为![]() 米,求函数
米,求函数![]() 的解析式;
的解析式;
(2)为使仓库总面积![]() 达到最大,正面铁栅应设计为多长?
达到最大,正面铁栅应设计为多长?
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求第3,4,5组的频率;
(2)为了了解最优秀学生的情况,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com