
科目: 来源: 题型:
【题目】已知抛物线C1:y2=2px(p>0)的焦点为F,抛物线上存在一点G到焦点的距离为3,且点G在圆C:x2+y2=9上. (Ⅰ)求抛物线C1的方程;
(Ⅱ)已知椭圆C2: ![]() =1(m>n>0)的一个焦点与抛物线C1的焦点重合,且离心率为
=1(m>n>0)的一个焦点与抛物线C1的焦点重合,且离心率为 ![]() .直线l:y=kx﹣4交椭圆C2于A、B两个不同的点,若原点O在以线段AB为直径的圆的外部,求k的取值范围.
.直线l:y=kx﹣4交椭圆C2于A、B两个不同的点,若原点O在以线段AB为直径的圆的外部,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2。设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O![]() LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .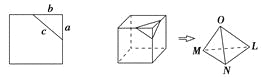
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形. 
(1)求证:AD⊥PB;
(2)已知点M是线段PC上,MC=λPM,且PA∥平面MQB,求实数λ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图(1)为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人. (Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;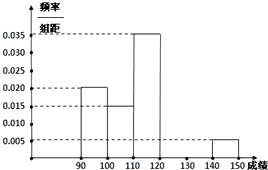
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面2×2
列联表(即填写空格处的数据),并判断是否有99%的把握认为“进入决赛的同学
成为种子选手与专家培训有关”.
| [140,150] | 合计 | |
参加培训 | 5 | 8 | |
未参加培训 | |||
合计 | 4 |
附: ![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足a1=1,a2=4,且对任意m,n,p,q∈N* , 若m+n=p+q,则有am+an=ap+aq . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{ ![]() }的前n项和为Sn , 求证:
}的前n项和为Sn , 求证: ![]() ≤Sn<
≤Sn< ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}(n≥1,n∈N)满足a1=2,a2=6,且(an+2﹣an+1)﹣(an+1﹣an)=2,若[x]表示不超过x的最大整数,则[ ![]() +
+ ![]() +…+
+…+ ![]() ]= .
]= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
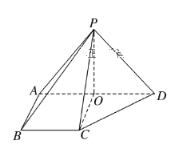
(1)求B点到平面PCD的距离;
(2)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com