
科目: 来源: 题型:
【题目】四棱锥P﹣ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=﹣2xln(1+
,g(x)=﹣2xln(1+ ![]() )﹣lnf(x).
)﹣lnf(x).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,函数g(x)在定义域内是否存在零点?如果存在,求出该零点;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,设圆的方程为(x+2 ![]() )2+y2=48,F1是圆心,F2(2
)2+y2=48,F1是圆心,F2(2 ![]() ,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设直线l(与x轴不重合)与曲线C交于A、B两点,与x轴交于点M.
(i)是否存在定点M,使得 ![]() +
+ ![]() 为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
(ii)在满足(i)的条件下,连接并延长AO交曲线C于点Q,试求△ABQ面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源则是中国古代数学家祖冲之的圆周率.祖冲之,在世界数学史上第一次将圆周率(π)值计算到小数点后的第7位,即3.1415926到3.1415927之间,数列{an}是公差大于0的等差数列,其前三项是“31415926”中连续的三个数,数列{bn}是等比数列,其公比大于1的正整数且前三项是“31415926”中的三个数,且a3=b3 .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)cn= 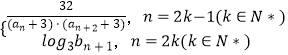 ,求c1+c2+c3+…+c
,求c1+c2+c3+…+c ![]() .(n∈N*)
.(n∈N*)
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的直三棱柱ABC﹣A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点. 
(Ⅰ)证明:DE∥平面A1B1C1;
(Ⅱ)求平面C1BD和平面CBD所成的角(锐角)的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高中组织数学知识竞赛,采取答题闯关的形式,分两种题型,每种题型设两关.“数学文化”题答对一道得5分,“数学应用”题答对一道得10分,答对一道题即可进入下一关,否则终止比赛.有甲、乙、丙三人前来参赛,设三人答对每道题的概率分别是 ![]() 、
、 ![]() 、
、 ![]() ,三人答题互不影响.甲、乙选择“数学文化”题,丙选择“数学应用”题.
,三人答题互不影响.甲、乙选择“数学文化”题,丙选择“数学应用”题.
(Ⅰ)求乙、丙两人所得分数相等的概率;
(Ⅱ)设甲、丙两人所得分数之和为随机变量X,求X的分布列与期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量 ![]() =(sin(π+ωx),2cosωx),
=(sin(π+ωx),2cosωx), ![]() =(2
=(2 ![]() sin(
sin( ![]() +ωx),cosωx),(ω>0),函数f(x)=
+ωx),cosωx),(ω>0),函数f(x)= ![]()
![]() ,其图象上相邻的两个最低点之间的距离为π.
,其图象上相邻的两个最低点之间的距离为π.
(Ⅰ)求函数f(x)的对称中心;
(Ⅱ)在锐角△ABC中,角A、B、C的对边分别为a、b、c,tanB= ![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=blnx+a(a>0,b>0)在x=1处的切线与圆(x﹣2)2+y2=4相交于A、B两点,并且弦长|AB|= 2 ![]() ,则
,则 ![]() +
+ ![]() ﹣
﹣ ![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有种不同的走法. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com