
科目: 来源: 题型:
【题目】如图, ![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】若实数数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(Ⅰ)若数列![]() 是
是![]() 数列,且
数列,且![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)求证:若数列![]() 是
是![]() 数列,则
数列,则![]() 的项不可能全是正数,也不可能全是负数;
的项不可能全是正数,也不可能全是负数;
(Ⅲ)若数列![]() 为
为![]() 数列,且
数列,且![]() 中不含值为零的项,记
中不含值为零的项,记![]() 前
前![]() 项中值为负数的项的个数为
项中值为负数的项的个数为![]() ,求
,求![]() 所有可能取值.
所有可能取值.
查看答案和解析>>
科目: 来源: 题型:
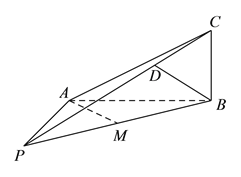
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,设点
中,设点![]() 是椭圆
是椭圆![]() :
: ![]() 上一点,从原点
上一点,从原点![]() 向圆
向圆![]() :
: ![]() 作两条切线分别与椭圆
作两条切线分别与椭圆![]() 交于点
交于点![]() ,
, ![]() ,直线
,直线![]() ,
, ![]() 的斜率分别记为
的斜率分别记为![]() ,
, ![]() .
.

(1)求证: ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
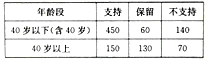
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:
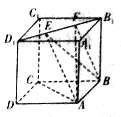
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com