
科目: 来源: 题型:
【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率![]() ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A,![]() 两点
两点![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,![]() ,过P、
,过P、![]() 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若![]() ,求圆Q的标准方程.
,求圆Q的标准方程.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
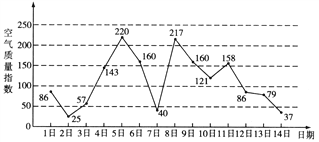
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P-ABCD中, PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1, ![]() ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
(Ⅰ)求证:AD⊥CG;
(Ⅱ)求平面BCP与平面DCP的夹角的余弦值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() 的关系,对某校高三某班学生进行了关注统计,得到如表数据:
的关系,对某校高三某班学生进行了关注统计,得到如表数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是
的线性回归方程,并预测答题正确率是![]() 的强化训练次数(保留整数);
的强化训练次数(保留整数);
(2)若用![]() (
(![]() )表示统计数据的“强化均值”(保留整数),若“强化均值”的标准差在区间
)表示统计数据的“强化均值”(保留整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
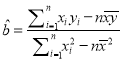 ,
, ![]() ,样本数据
,样本数据![]() ,
, ![]() ,…,
,…, ![]() 的标准差为
的标准差为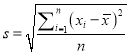
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,直线
,直线![]() .
.
(1)以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆![]() 和直线
和直线![]() 的交点的极坐标;
的交点的极坐标;
(2)若点![]() 为圆
为圆![]() 和直线
和直线![]() 交点的中点,且直线
交点的中点,且直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求
为参数),求![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com