【题目】已知曲线C1的参数方程为（t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为.

（1）求曲线C1的极坐标方程和C2的直角坐标方程；

（2）射线OP：（其中）与C2交于P点，射线OQ：与C2交于Q点，求的值.

【题目】已知函数

（1）求的零点；

（2）若有两个零点，求实数的取值范围.

（3）若有三个零点，求实数的取值范围.

在平面直角坐标系中，曲线的参数方程是（为参数，），在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程是，等边的顶点都在上，且点，，依逆时针次序排列，点的极坐标为.

（1）求点，，的直角坐标；

（2）设为上任意一点，求点到直线距离的取值范围.

【题目】如图，在多面体中，底面是边长为2的菱形，，四边形是矩形，和分别是和的中点.

（1）求证：平面平面；

（2）若平面平面，，求平面与平面所成角的余弦值.

【题目】对于函数，若在定义域内存在实数，满足，则称为“类函数”.

（1）已知函数，试判断是否为“类函数”？并说明理由；

（2）设是定义在上的“类函数”，求是实数的最小值；

（3）若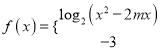 为其定义域上的“类函数”，求实数的取值范围.

【题目】已知函数和，

（Ⅰ）设，求函数的单调区间；

（Ⅱ）当时，为函数图象与函数图象的公共点，且在点处有公共切线，求点的坐标及实数的值．

【题目】生物学家预言，21世纪将是细菌发电造福人类的时代。说起细菌发电，可以追溯到1910年，英国植物学家利用铂作为电极放进大肠杆菌的培养液里，成功地制造出世界上第一个细菌电池。然而各种细菌都需在最适生长温度的范围内生长。当外界温度明显高于最适生长温度，细菌被杀死；如果在低于细菌的最低生长温度时，细菌代谢活动受抑制。为了研究某种细菌繁殖的个数是否与在一定范围内的温度有关，现收集了该种细菌的6组观测数据如下表：

经计算得：，，线性回归模型的残差平方和．其中分别为观测数据中的温度与繁殖数，.

参考数据：，，

（Ⅰ）求关于的线性回归方程（精确到0.1）；

（Ⅱ）若用非线性回归模型求得关于回归方程为，且非线性回归模型的残差平方和．

（ⅰ）用相关指数说明哪种模型的拟合效果更好；

（ⅱ）用拟合效果好的模型预测温度为34℃时该种细菌的繁殖数（结果取整数）.

附：一组数据，其回归直线的斜率和截距的最小二乘法估计为，；

相关指数

【题目】是上奇函数，对任意实数都有，当时，，则 （ ）

A. －1B. 1C. 0D. 2

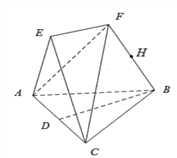
【题目】如图，在三棱锥与三棱锥中，和都是边长为2的等边三角形，分别为的中点，，．

（Ⅰ）试在平面内作一条直线，当时，均有平面（作出直线并证明）；

（Ⅱ）求两棱锥体积之和的最大值.