
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出以下命题:
①双曲线![]() 的渐近线方程为y=±
的渐近线方程为y=±![]() x;
x;
②命题p:“x∈R,sinx+![]() ≥2”是真命题;
≥2”是真命题;
③已知线性回归方程为![]() =3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
=3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,则P(-1<ξ<0)=0.6;
⑤设![]() ,则
,则![]()
则正确命题的序号为________(写出所有正确命题的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)用分段函数的形式表示函数f(x);
(2)在平面直角坐标系中画出函数f(x)的图象;

(3)在同一平面直角坐标系中,再画出函数g(x)=![]() (x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)>
(x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)> ![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)若a=1,b=2,求函数在点(2,f(2))处的切线方程;
(2)求函数的单调区间;
(3)若a<b,任取![]() 存在实数m使
存在实数m使![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
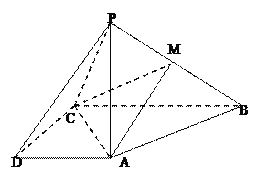
【题目】如图,在四棱锥![]() 中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.
中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.
(1)求证:AM||平面PCD;
(2)求证:平面ACM⊥平面PAB;
(3)若PC与平面ACM所成角为30°,求PA的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为![]() 个,零件的实际出厂单价为
个,零件的实际出厂单价为![]() 元.写出函数
元.写出函数![]() 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】湖南省某自来水公司每个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过30吨时,按每吨2元收取;当该用户用水量超过30吨但不超过50吨时,超出部分按每吨3元收取;当该用户用水量超过50吨时,超出部分按每吨4元收取。
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为214元,且甲、乙两用户用水量之比为3:2,试求出甲、乙两用户在该收费周期内各自的用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com