
科目: 来源: 题型:
【题目】为积极响应国家“阳光体育运动”的号召,某学校在了解到学生的实际运动情况后,发起以“走出教室,走到操场,走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况,从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样,收集300位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图。

(1)据图估计该校学生每周平均体育运动时间.并估计高一年级每周平均体育运动时间不足4小时的人数;
(2)规定每周平均体育运动时间不少于6小时记为“优秀”,否则为“非优秀”,在样本数据中,有30位高三学生的每周平均体育运动时间不少于6小时,请完成下列![]() 列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中,选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15
的值一定是15
B. 两个变量相关性越强,则相关系数![]() 就越接近于1
就越接近于1
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关
D. 若某商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元/件)存在线性回归方程为
(元/件)存在线性回归方程为![]() ,当销售价格为10元时,销售量为100件左右
,当销售价格为10元时,销售量为100件左右
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的任意三个顶点为顶点的三角形的面积是
的任意三个顶点为顶点的三角形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的右顶点,点
的右顶点,点![]() 在
在![]() 轴上.若椭圆
轴上.若椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)有物理、化学、生物三个学科竞赛各设冠军一名,现有![]() 人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
(2)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
(3)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 的右顶点,过点
的右顶点,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
, ![]() 两点.求证:点
两点.求证:点![]() 在以
在以![]() 为直径的圆上.
为直径的圆上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.若猫眼曲线
为“猫眼曲线”.若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() .
.
(1)求猫眼曲线![]() 的方程;
的方程;
(2)任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为
所得弦的中点为![]() ,交椭圆
,交椭圆![]() 所得弦的中点为
所得弦的中点为![]() ,求证:
,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.

(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;
(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
【答案】(1) ![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先根据三角函数平方关系消参数得曲线![]() ,再根据
,再根据![]() 将曲线
将曲线![]() 的
的![]() 极坐标方程;(2)将
极坐标方程;(2)将![]() 代人曲线
代人曲线![]() 的极坐标方程,再根据
的极坐标方程,再根据![]() 求
求![]() .
.
试题解析:(1)曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
可化为普通方程![]() ,
,
由![]() ,可得曲线
,可得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径为
的极径为![]() ,
,
射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径满足
的极径满足![]() ,解得
,解得![]() ,
,
所以![]() .
.
【题型】解答题
【结束】
23
【题目】设函数![]() .
.
(1)设![]() 的解集为
的解集为![]() ,求集合
,求集合![]() ;
;
(2)已知![]() 为(1)中集合
为(1)中集合![]() 中的最大整数,且
中的最大整数,且![]() (其中
(其中![]() ,
,![]() ,
,![]() 为正实数),求证:
为正实数),求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 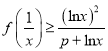 ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据切线过点
,再根据切线过点![]() ,解得
,解得![]() 导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为
导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为![]() ,分离得
,分离得![]() ,再利用导数求函数
,再利用导数求函数![]() 单调性,利用罗伯特法则求最大值,即得
单调性,利用罗伯特法则求最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,即
,即![]()
由题意得![]() ,解得
,解得![]()
所以![]()
从而![]()
因为当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在区间
在区间![]() 上是减函数,区间
上是减函数,区间![]() 上是增函数,
上是增函数,
从而![]() .
.
(2)由题意知,当![]() 时,
时, ![]() ,所以
,所以![]()
从而当![]() 时,
时, ![]() ,
,
由题意知 ,即
,即![]() ,其中
,其中![]()
设![]() ,其中
,其中![]()
设![]() ,即
,即![]() ,其中
,其中![]()
则![]() ,其中
,其中![]()
(1)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是增函数
是增函数
从而当![]() 时,
时, ![]() ,
,
所以![]() 是增函数,从而
是增函数,从而![]() .
.
故当![]() 时符合题意.
时符合题意.
(2)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是减函数
上是减函数
从而当![]() 时,
时, ![]()
所以![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]()
故当![]() 时不符合题意.
时不符合题意.
(3)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是减函数
是减函数
从而当![]() 时,
时, ![]()
所以![]() 是减函数,从而
是减函数,从而![]()
故当![]() 时不符合题意
时不符合题意
综上![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
22
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com