
科目: 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
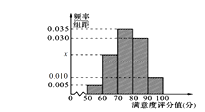
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目: 来源: 题型:
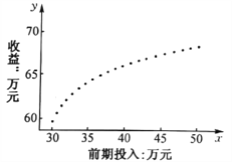
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近期前期广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共
(单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共![]() 个数据点)及一些统计量的值.为了进一步了解广告投入量
个数据点)及一些统计量的值.为了进一步了解广告投入量![]() 对收益
对收益![]() 的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
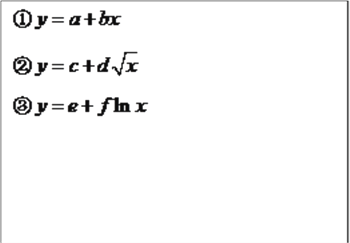
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据![]() ,
, ![]() ,参考数据:
,参考数据: ![]() ,
, ![]() .
.
(1)根据散点图判断,哪一位员工提出的模型不适合用来描述![]() 与
与![]() 之间的关系?简要说明理由.
之间的关系?简要说明理由.
(2)根据(1)的判断结果及表中数据,在余下两个模型中分别建立收益![]() 关于投入量
关于投入量![]() 的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益
的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益![]() 的回归方程)?说明理由;
的回归方程)?说明理由;
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率、截距的最小二乘估计以及相关系数分别为:
的斜率、截距的最小二乘估计以及相关系数分别为:
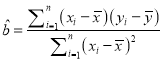 ,
, ![]() ,
, 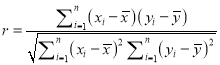 ,
,
其中![]() 越接近于
越接近于![]() ,说明变量
,说明变量![]() 与
与![]() 的线性相关程度越好.
的线性相关程度越好.
查看答案和解析>>
科目: 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
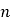
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
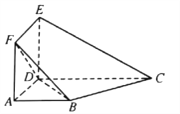
【题目】如图,某几何体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 是直角梯形,
是直角梯形, ![]() 是直角,
是直角, ![]() ,
, ![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数y=f(x)对定义域内的每一个值x1,在其定义域内都存在唯一的x2,使f(x1)f(x2)=1成立,则称该函数为“依赖函数”.
(1) 判断函数g(x)=2x是否为“依赖函数”,并说明理由;
(2) 若函数f(x)=(x–1)2在定义域[m,n](m>1)上为“依赖函数”,求实数m、n乘积mn的取值范围;
(3) 已知函数f(x)=(x–a)2 (a<![]() )在定义域[
)在定义域[![]() ,4]上为“依赖函数”.若存在实数x[
,4]上为“依赖函数”.若存在实数x[![]() ,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A≠0,ω>0,![]() <φ<
<φ<![]() )的图象关于直线
)的图象关于直线![]() 对称,它的最小正周期为π,则( )
对称,它的最小正周期为π,则( )
A. f(x)的图象过点(0,![]() ) B. f(x)在
) B. f(x)在![]() 上是减函数
上是减函数
C. f(x)的一个对称中心是![]() D. f(x)的一个对称中心是
D. f(x)的一个对称中心是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com