【题目】数列满足：

（1）求的值；

（2）求证：数列是等差数列，并求数列的通项公式；

（3）设假设恒成立，求实数的取值范围.

【题目】“克拉茨猜想”又称“猜想”，是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想：任给一个正整数，如果是偶数，就将它减半；如果为奇数就将它乘3加1,不断重复这样的运算，经过有限步后，最终都能够得到1.己知正整数经过6次运算后得到1，则的值为__________．

【题目】为普及学生安全逃生知识与安全防护能力，某学校高一年级举办了安全知识与安全逃生能力竞赛，该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛，现将所有参赛选手参加笔试的成绩（得分均为整数，满分为分）进行统计，制成如下频率分布表.

（1）求表中，，，，的值；

（2）按规定，预赛成绩不低于分的选手参加决赛.已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为，求的分布列和数学期望.

经验表明，最佳乐观系数x恰好使得（c﹣a）是（b﹣c）和（b﹣a）的等比中项，据此可得，最佳乐观系数x的值等于 ．

根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率．

（1）求出乙生产三等品的概率；

（2）求出甲生产一件产品，盈利不小于30元的概率；

（3）若甲、乙一天生产产品分别为40件和30件，估计甲、乙两人一天共为企业创收多少元？

A.12种B.24种C.36种D.48种

【题目】某校高一组织一次数学竞赛，选取50名学生成绩（百分制，均为整数），根据这50名学生的成绩，绘制频率分布直方图（如图所示），其中样本数据分组区间为．

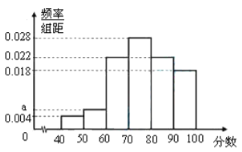
（1）求频率分布直方图中a的值；

（2）估计选取的50名学生在这次数学竞赛中的平均成绩；

（3）用分层抽样的方法在分数段为的学生成绩中抽取一个样本容量为5的样本，

再随机抽取2人的成绩，求恰有一人成绩在分数段内的概率．

【题目】如图，在棱长为1的正方体中，点分别是棱，的中点，是侧面内一点，若 平面，则线段长度的取值范围是（ ）

A. B. C. D.

（1）从3月1日至3月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均不小于27”的概率．

（2）若选取的是3月1日与3月5日的两组数据，请根据3月2日至3月4日的数据，求出y关于x的线性回归方程．

（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？

（参考公式：回归直线的方程是，其中，）

（1）在这一月生产的饮水机中，用分层抽样的方法抽取n台，其中有A类产品49台，求n的值；

（2）用随机抽样的方法，从C类经济型饮水机中抽取10台进行质量检测，经检测它们的得分如下：7.9，9.4，7.8，9.4，8.6，9.2，10，9.4，7.9，9.4，从D类经济型饮水机中抽取10台进行质量检测，经检测它们的得分如下：8.9，9.3，8.8，9.2，8.6，9.2，9.0，9.0，8.4，8.6，根据分析，你会选择购买C类经济型饮水机与D类经济型饮水机中哪类产品.