已知函数（其中a是实数）．

（1）求的单调区间；

（2）若设，且有两个极值点 ，求取值范围．（其中e为自然对数的底数）．

【题目】某医疗器械公司在全国共有个销售点，总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这个销售点的年销量绘制出如下的频率分布直方图.

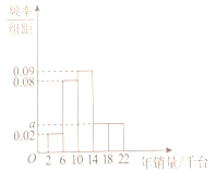
（1）完成年销售任务的销售点有多少个？

（2）若用分层抽样的方法从这个销售点中抽取容量为的样本，求该五组，，，，，（单位：千台）中每组分别应抽取的销售点数量.

（3）在（2）的条件下，从前两组，中的销售点随机选取个，记这个销售点在中的个数为，求的分布列和期望.

【题目】已知椭圆的半焦距为，圆与椭圆有且仅有两个公共点，直线与椭圆只有一个公共点.

（1）求椭圆的标准方程；

（2）已知动直线过椭圆的左焦点，且与椭圆分别交于两点，试问：轴上是否存在定点，使得为定值?若存在，求出该定值和点的坐标；若不存在，请说明理由.

【题目】已知函数。

（1）当时，求函数在点处的切线方程；

（2）若函数，讨论函数的单调性；

（3）若（2）中函数有两个极值点，且不等式恒成立，求实数的取值范围.

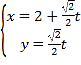【题目】在极坐标系中，曲线的极坐标方程为.现以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程为(为参数).

（1）求曲线的直角坐标系方程和直线的普通方程；

（2）点在曲线上，且到直线的距离为，求符合条件的点的直角坐标.

【题目】一个盒子里装有大小均匀的个小球，其中有红色球个，编号分别为；白色球个, 编号分别为, 从盒子中任取个小球（假设取到任何—个小球的可能性相同）．

（1）求取出的个小球中，含有编号为的小球的概率；

（2）在取出的个小球中, 小球编号的最大值设为，求随机变量的分布列．

【题目】已知函数．

（1）那么方程在区间上的根的个数是___________．

（2）对于下列命题：

①函数是周期函数；

②函数既有最大值又有最小值；

③函数的定义域是，且其图象有对称轴；

④在开区间上，单调递减．

其中真命题的序号为______________（填写真命题的序号）．

在直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

（1）写出曲线的普通方程和曲线的直角坐标方程；

（2）已知点是曲线上的动点，求点到曲线的最小距离．

(1)求数列的前三项，60是此数列的第几项？

(2)n为何值时，an＝0，an>0，an<0?

(3)该数列前n项和Sn是否存在最值？说明理由．