
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在
时,是否存在![]() ,使得
,使得![]() 和
和![]() 的图象在
的图象在![]() 处的切线互相平行,若存在,请给予证明,若不存在,请说明理由
处的切线互相平行,若存在,请给予证明,若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]()
![]() 的最小正周期为
的最小正周期为![]() ,若其图像向左平移
,若其图像向左平移![]() 个单位后得到的函数为偶函数,则函数
个单位后得到的函数为偶函数,则函数![]() 的图像( )
的图像( )
A. 关于点![]() 对称 B. 关于点
对称 B. 关于点![]() 对称 C. 关于直线
对称 C. 关于直线![]() 对称 D. 关于直线
对称 D. 关于直线![]() 对称
对称
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。”,意思是:“假设一个刍童,上底面宽1尺,长2尺;下底面宽3尺,长4尺,高1尺(如图)。”(注:刍童为上下底面为相互平行的不相似长方形,两底面的中心连线与底面垂直的几何体),若该几何体所有顶点在一球体的表面上,则该球体的表面积为( )
A. ![]() 平方尺 B.
平方尺 B. ![]() 平方尺 C.
平方尺 C. ![]() 平方尺 D.
平方尺 D. ![]() 平方尺
平方尺
查看答案和解析>>
科目: 来源: 题型:
【题目】已知从![]() 地到
地到![]() 地有两条道路可以到达,走道路①准点到达的概率为
地有两条道路可以到达,走道路①准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() ;走道路②准点到达的概率为
;走道路②准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() .若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
.若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
(1)若三辆车中恰有一辆车没有准点到达的概率为![]() ,求走道路②准点到达的概率
,求走道路②准点到达的概率![]() ;
;
(2)在(1)的条件下,求三辆车中准点到达车辆的辆数的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为108万元,铺设距离为![]() 千米的相邻两增压站之间的输油管道费用为
千米的相邻两增压站之间的输油管道费用为![]() 万元.设余下工程的总费用为
万元.设余下工程的总费用为![]() 万元.
万元.
(1)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(2)需要修建多少个增压站才能使总费用![]() 最小?
最小?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定点M(-3,0),Q、P分别是x轴、y轴上的动点,且使MP⊥PQ,点N在直线PQ上,![]()
(1)求动点N的轨迹C的方程.
(2)过点T(-1,0)作直线l与轨迹C交于两点A、B,问:在x轴上是否存在一点D,使△ABD为等边三角形;若存在,试求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】正五边形![]() 的对角线
的对角线![]() 分别与对角线
分别与对角线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,对角线
,对角线![]() 分别与对角线
分别与对角线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,对角线
,对角线![]() 与对角线
与对角线![]() 交于点
交于点![]() . 设由图2中的10个点
. 设由图2中的10个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和线段构成的等腰三角形的集合为
和线段构成的等腰三角形的集合为![]() .
.
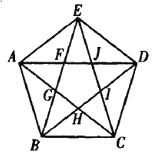
(1)求![]() 中元素的数目;
中元素的数目;
(2)若将这10个点中的每个点任意染为红、蓝两种颜色之一,问是否一定存在![]() 中的一个等腰三角形,其三个顶点同色?
中的一个等腰三角形,其三个顶点同色?
(3)若将这10个点中的任意![]() 个点染为红色,使得一定存在
个点染为红色,使得一定存在![]() 中的一个等腰三角形,其三个顶点同为红色,求
中的一个等腰三角形,其三个顶点同为红色,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,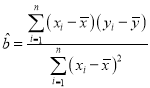
参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com