
科目: 来源: 题型:
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题“若
”的逆否命题“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
其中错误的是__________.(填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆周上有七个不同的点,以其中任意一点为始点,另一点为终点作向量,作出所有的向量(对于点![]() 、
、![]() ,若作出向量
,若作出向量![]() ,则不再作向量
,则不再作向量![]() ).若其中某四点所确定的凸四边形的四条边是首尾相接的四个向量,则称其为“零四边形”.试求以这七个点中四个点为顶点的凸四边形中,零四边形个数的最大值
).若其中某四点所确定的凸四边形的四条边是首尾相接的四个向量,则称其为“零四边形”.试求以这七个点中四个点为顶点的凸四边形中,零四边形个数的最大值
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为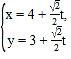 (
(![]() 为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且设定点
两点,且设定点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研究新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品B研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利ξ万元的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() ,得曲线
,得曲线![]() .
.
(1)求出![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】画糖人是一种以糖为材料在石板上进行造型的民间艺术.某糖人师傅在公园内画糖人,每天卖出某种糖人的个数与价格相关,其相关数据统计如下表:
每个糖人的价格 | 9 | 10 | 11 | 12 | 13 |
卖出糖人的个数 | 54 | 50 | 46 | 43 | 39 |
(1)根据表中数据求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若该种造型的糖人的成本为2元/个,为使糖人师傅每天获得最大利润,则该种糖人应定价多少元?(精确到1元)
参考公式:回归直线方程![]() ,其中
,其中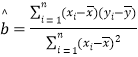 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
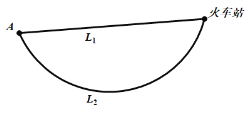
【题目】如图,![]() 地到火车站共有两条路径,据统计两条路径所用的时间互不影响,所用时间在各时间段内的的频率如下表:
地到火车站共有两条路径,据统计两条路径所用的时间互不影响,所用时间在各时间段内的的频率如下表:
时间(分钟) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现甲、乙两人分别有![]() 分钟和
分钟和![]() 分钟时间用于赶往火车站.
分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用![]() 表示甲、乙两人中在允许的时间内赶到火车站的人数,针对(1)的选择方案,求
表示甲、乙两人中在允许的时间内赶到火车站的人数,针对(1)的选择方案,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】新冠状病毒严重威胁着人们的身体健康,我国某医疗机构为了调查新冠状病毒对我国公民的感染程度,选了某小区的![]() 位居民调查结果统计如下:
位居民调查结果统计如下:
感染 | 不感染 | 合计 | |
年龄不大于 |
| ||
年龄大于 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为感染新冠状病与不同年龄有关?
的前提下认为感染新冠状病与不同年龄有关?
(3)已知在被调查的年龄大于![]() 岁的感染者中有
岁的感染者中有![]() 名女性,其中
名女性,其中![]() 位是女教师,现从这
位是女教师,现从这![]() 名女性中随机抽取
名女性中随机抽取![]() 人,求至多有
人,求至多有![]() 位教师的概率.
位教师的概率.
附: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com