
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 上恰有2个点到
上恰有2个点到![]() 的距离等于
的距离等于![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月13日《西安市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
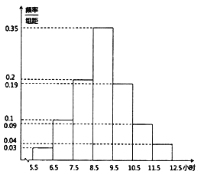
(1)求这200名学生每周阅读时间的样本平均数;
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附: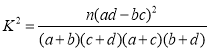 (
(![]() ).
).
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的上焦点,
的上焦点,![]() 上一点
上一点![]() 在
在![]() 轴上方,且
轴上方,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)![]() 为直线
为直线![]() 与
与![]() 异于
异于![]() 的交点,
的交点,![]() 的弦
的弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,若
,若![]() 在同一直线上,求
在同一直线上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产一种产品,从流水线上随机抽取100件产品,统计其质量指数并绘制频率分布直方图(如图1):
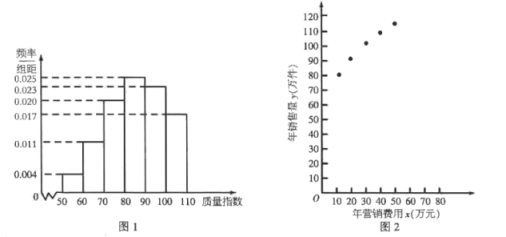
产品的质量指数在![]() 的为三等品,在
的为三等品,在![]() 的为二等品,在
的为二等品,在![]() 的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年的年营销费用
(单位:万件)的影响,对近5年的年营销费用![]() 和年销售量
和年销售量![]()
![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中![]() ,
,![]() ,
,![]() ,
,![]()
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
(ⅰ)建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取![]() )
)
参考公式:对于一组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小乘估计分别为
的斜率和截距的最小乘估计分别为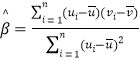 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 满足以
满足以![]() 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 过右焦点
过右焦点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值?如果存在,求出点
为定值?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com