【题目】如图，的内心为，、、分别是边、、的中点，证明：直线平分的周长．

【题目】求最小的正整数，使得当正整数点时，在前个正整数构成的集合中，对任意总存在另一个数且，满足为平方数．

【题目】已知在正整数n的各位数字中，共含有个1，个2，，个n．证明：并确定使等号成立的条件．

【题目】已知梯形中，,,,,是上的点，是的中点，沿将梯形折起，使平面平面.

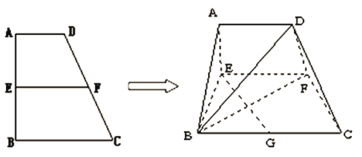
（1）当时，求证：；

（2）记以为顶点的三棱锥的体积为，求的最大值；

（3）当取得最大值时，求二面角的大小.

(1) 证明：PB∥平面AEC

(2) 设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积

【题目】如图，已知平面，点为的中点.

（1）求证：平面平面；

（2）求直线与平面所成角的大小.

【题目】如果从北大打车到北京车站去接人，聪明的专家一定会选择走四环。虽然从城中间直穿过去看上去很诱人，但考虑到北京的道路几乎总是正南正北的方向，事实上不会真有人认为这样走能抄近路。在城市中，专家估算两点之间的距离时，不会直接去测量两点之间的直线距离，而会去考虑它们相距多少个街区。在理想模型中，假设每条道路都是水平或者竖直的，那么只要你朝着目标走（不故意绕远路），不管你这样走，花费的路程都是一样的。出租车几何学（taxicab geometry），所谓的“出租车几何学”是由十九世纪的另一位真专家赫尔曼-闵可夫斯基所创立的。在出租车几何学中，点还是形如的有序实数对，直线还是满足的所有组成的图形，角度大小的定义也和原来一样。只是直角坐标系内任意两点，定义它们之间的一种“距离”：，请解决以下问题：

（1）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点的“距离”均为的“圆”方程，并作出大致图像；

（2）在出租车几何学中，到两点、“距离”相等的点的轨迹称为线段的“垂直平分线”，已知点，，；

①写出在线段的“垂直平分线”的轨迹方程，并写出大致图像；

②求证：三边的“垂直平分线”交于一点（该点称为的“外心”），并求出的“外心”.

【题目】某厂生产某种产品的年固定成本为250万元，每生产千件，需另投入成本，当年产量不足80千件时，（万元）；当年产量不小于80千件时，（万元），每件售价为0.05万元，通过市场分析，该厂生产的商品能全部售完．

（1）写出年利润（万元）关于年产量（千件）的函数解析式；

（2）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

【题目】已知椭圆上一点关于原点的对称点为，为其右焦点，若，设，且，则该椭圆的离心率的取值范围是( )

A. B.

C. D.

【题目】（多选题）设正实数满足，则（）

A. 有最小值4B. 有最小值

C. 有最大值D. 有最小值