
科目: 来源: 题型:
【题目】已知函数f(x)=(kx+![]() )ex﹣2x,若f(x)<0的解集中有且只有一个正整数,则实数k的取值范围为 ( )
)ex﹣2x,若f(x)<0的解集中有且只有一个正整数,则实数k的取值范围为 ( )
A. [![]() ,
,![]() )B. (
)B. (![]() ,
,![]() ]
]
C. [![]() )D. [
)D. [![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() :曲线
:曲线![]() 表示双曲线;
表示双曲线;![]() :曲线
:曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆.
轴上的椭圆.
(1)分别求出条件![]() 中的实数
中的实数![]() 的取值范围;
的取值范围;
(2)甲同学认为“![]() 是
是![]() 的充分条件”,乙同学认为“
的充分条件”,乙同学认为“![]() 是
是![]() 的必要条件”,请判断两位同学的说法是否正确,并说明理由.
的必要条件”,请判断两位同学的说法是否正确,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业用180万元购买一套新设备,该套设备预计平均每年能给企业带来100万元的收入,为了维护设备的正常运行,第一年需要各种维护费用10万元,且从第二年开始,每年比上一年所需的维护费用要增加10万元
(1)求该设备给企业带来的总利润![]() (万元)与使用年数
(万元)与使用年数![]() 的函数关系;
的函数关系;
(2)试计算这套设备使用多少年,可使年平均利润最大?年平均利润最大为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角为
,倾斜角为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于两点
,且与抛物线交于两点![]() 、
、![]() .
.
(1)求抛物线的标准方程及准线方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的中垂线
的中垂线![]() 交
交![]() 轴于点
轴于点![]() .证明:
.证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
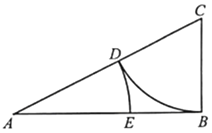
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中已知A(4,O)、B(0,2)、C(-1,0)、D(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
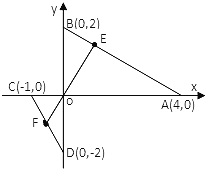
(1)若F为线段CD的中点,证明:![]() ;
;
(2)“若F为线段CD的中点,则![]() ”的逆命题是否成立?说明理由;
”的逆命题是否成立?说明理由;
(3)设![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有![]() 多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的
多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的![]() 件工艺品测得重量(单位:
件工艺品测得重量(单位:![]() )数据如下表:
)数据如下表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合计 |
|
(1)求出频率分布表中实数![]() ,
,![]() 的值;
的值;
(2)若从仿制的![]() 件工艺品重量范围在
件工艺品重量范围在![]() 的工艺品中随机抽选
的工艺品中随机抽选![]() 件,求被抽选
件,求被抽选![]() 件工艺品重量均在范围
件工艺品重量均在范围![]() 中的概率.
中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等轴双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 在直线
在直线![]() 上,线段
上,线段![]() 的中点是坐标原点,且双曲线经过点
的中点是坐标原点,且双曲线经过点![]() .
.
(1)若已知下列所给的三个方程中有一个是等轴双曲线![]() 的方程:①
的方程:①![]() ;②
;②![]() ;③
;③![]() .请推理判断哪个是等轴双曲线
.请推理判断哪个是等轴双曲线![]() 的方程,并求出此双曲线的实轴长;
的方程,并求出此双曲线的实轴长;
(2)现要在等轴双曲线![]() 上选一处
上选一处![]() 建一座码头,向
建一座码头,向![]() 、
、![]() 两地转运货物.经测算,从
两地转运货物.经测算,从![]() 到
到![]() 、从
、从![]() 到
到![]() 修建公路的费用都是每单位长度
修建公路的费用都是每单位长度![]() 万元,则码头应建在何处,才能使修建两条公路的总费用最低?
万元,则码头应建在何处,才能使修建两条公路的总费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com