
科目: 来源: 题型:
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
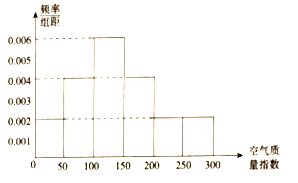
(1)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(2)从这10天的空气质量指数监测数据中,随机抽取三天,求恰好有一天空气质量良的概率;
(3)从这10天的数据中任取三天数据,记![]() 表示抽取空气质量良的天数,求
表示抽取空气质量良的天数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
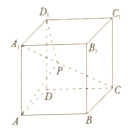
【题目】如图,在正方体![]() 中,棱长为1,点
中,棱长为1,点![]() 为线段
为线段![]() 上的动点(包含线段端点),则下列结论错误的是( )
上的动点(包含线段端点),则下列结论错误的是( )
A. 当![]() 时,
时,![]() 平面
平面![]()
B. 当![]() 为
为![]() 中点时,四棱锥
中点时,四棱锥![]() 的外接球表面为
的外接球表面为![]()
C. ![]() 的最小值为
的最小值为![]()
D. 当![]() 时,
时,![]() 平面
平面![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() .
.
(1)若直线![]() 不经过第四象限,求
不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,
,![]() 为坐标原点,设
为坐标原点,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
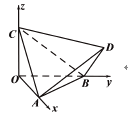
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】给出三个命题:①直线上有两点到平面的距离相等,则直线平行平面;②夹在两平行平面间的异面直线段的中点的连线平行于这个平面;③过空间一点必有唯一的平面与两异面直线平行.正确的是( )
A. ②③B. ①②C. ①②③D. ②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com