（1）求B；

（2）已知b＝4，△ABC的面积为，求△ABC的周长．

（1）设a＝4，求过点A且与圆C相切的直线方程；

（2）设a＝3，直线l过点A且被圆C截得的弦长为，求直线l的方程．

【题目】F1，F2是椭圆C1和双曲线C2的公共焦点，e1，e2分别为曲线C1，C2的离心率，P为曲线C1，C2的一个公共点，若，且，则e1∈_____．

【题目】定义在上的函数满足，．

(1)求函数的单调区间；

(2)如果，且，求证：．

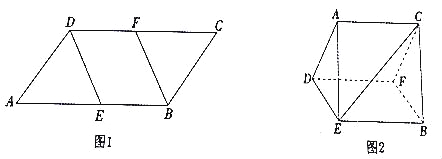
【题目】如图1，在平行四边形中，，，点是的中点，点是的中点，分别沿．将和折起，使得平面平面（点在平面的同侧），连接，如图2所示．

（1）求证：；

（2）当，且平面平面时，求三棱锥的体积．

【题目】已知函数=．

(1)求函数的单调递增区间；

(2)已知在△ABC中，A，B，C的对边分别为a，b，c，若,，求.

【题目】设各项均为正数的数列{an}的前n项和为Sn，满足：对任意的n∈N*，都有an+1+Sn+1＝1，又a1．

（1）求数列{an}的通项公式；

（2）令bn＝log2an，求（n∈N*）

【题目】在如图所示的五面体中， ， ， ，四边形是正方形，二面角的大小为．

（1）在线段上找出一点，使得平面，并说明理由；

（2）求直线与平面所成角的正弦值．

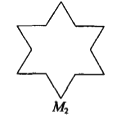（1）（2）（3）.

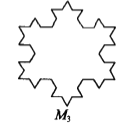设图（1）的等边三角形的边长为1，并且分别将图（1）、（2）、（3）…中的图形依次记作M1、M2、M3、……

（1）设中的边数为中每条边的长度为，写出数列和的递推公式与通项公式；

（2）设的周长为，所围成的面积为，求数列{}与{}的通项公式；请问周长与面积的极限是否存在？若存在，求出该极限，若不存在，简单说明理由.

【题目】设圆的圆心为，直线过点且与轴不重合，直线交圆于，两点，过点作的平行线交于点.

（1）证明为定值，并写出点的轨迹方程；

（2）设点的轨迹为曲线，直线交于，两点，过点且与直线垂直的直线与圆交于，两点，求四边形面积的取值范围.