【题目】在平面直角坐标系中，如果与都是整数，就称点为整点，下列命题中正确的是_____________（写出所有正确命题的编号）

①存在这样的直线，既不与坐标轴平行又不经过任何整点

②如果与都是无理数，则直线不经过任何整点

③直线经过无穷多个整点，当且仅当经过两个不同的整点

④直线经过无穷多个整点的充分必要条件是：与都是有理数

⑤存在恰经过一个整点的直线

【题目】已知的内角、、的对边分别为、、，为内一点，若分别满足下列四个条件：

①；

②；

③；

④；

则点分别为的（ ）

A.外心、内心、垂心、重心B.内心、外心、垂心、重心

C.垂心、内心、重心、外心D.内心、垂心、外心、重心

【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足升的,按升计算(如剩余升,记为剩余升).例如:结账时,某桌剩余酒量恰好为升,则该桌的每位客人还应付元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的组数据(其中表示饮酒人数,(升)表示饮酒量):,,,,.

（1）求由这组数据得到的关于的回归直线方程;

（2）小王约了位朋友坐在一桌饮酒,小王及朋友用量杯共量取了升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请位或位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议？

参考数据:回归直线的方程是,其中,.

【题目】已知椭圆()的左、右焦点分别是，，点为的上顶点，点在上，，且.

（1）求的方程；

（2）已知过原点的直线与椭圆交于，两点，垂直于的直线过且与椭圆交于，两点，若，求.

【题目】已知抛物线过点，是抛物线上异于点的不同两点，且以线段为直径的圆恒过点.

（I）当点与坐标原点重合时，求直线的方程；

（II）求证：直线恒过定点，并求出这个定点的坐标.

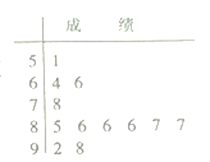
（1）求这组数据的众数和平均数；

（2）在这12名学生中从测试成绩介于80~90之间的学生中任选2人，求至少有1人“达标”的概率.

【题目】某学校为了解高一新生的体质健康状况，对学生的体质进行了测试. 现从男、女生中各随机抽取人，把他们的测试数据，按照《国家学生体质健康标准》整理如下表. 规定：数据≥，体质健康为合格.

(I)从样本中随机选取一名学生，求这名学生体质健康合格的概率；

(II)从男生样本和女生样本中各随机选取一人，求恰有一人的体质健康等级是优秀的概率；

（III）表中优秀、良好、及格、不及格四个等级的男生、女生平均分都接近（二者之差的绝对值不大于），但男生的总平均分却明显高于女生的总平均分．研究发现，若去掉四个等级中一个等级的数据，则男生、女生的总平均分也接近，请写出去掉的这个等级．（只需写出结论）

【题目】如图，在四棱锥中，底面为矩形，平面平面,,，，为中点．

（Ⅰ）求证：∥平面；

（Ⅱ）求二面角的余弦值；

（Ⅲ）在棱上是否存在点，使得？若存在，求的值；若不存在，说明理由．

【题目】已知平面内两个定点和点，是动点，且直线,的斜率乘积为常数，设点的轨迹为.

① 存在常数，使上所有点到两点距离之和为定值；

② 存在常数，使上所有点到两点距离之和为定值；

③ 不存在常数，使上所有点到两点距离差的绝对值为定值；

④ 不存在常数，使上所有点到两点距离差的绝对值为定值.

其中正确的命题是_______________.（填出所有正确命题的序号）

【题目】2019年3月2日，昌平 “回天”地区开展了种不同类型的 “三月雷锋月,回天有我”社会服务活动. 其中有种活动既在上午开展、又在下午开展， 种活动只在上午开展，种活动只在下午开展 . 小王参加了两种不同的活动，且分别安排在上、下午，那么不同安排方案的种数是___________.