
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,并且经过点
的焦点重合,并且经过点![]() .
.
(Ⅰ)求椭圆C的标准方程;
(II) 设椭圆C短轴的上顶点为P,直线![]() 不经过P点且与
不经过P点且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线PA与直线PB的斜率的和为
两点,若直线PA与直线PB的斜率的和为![]() ,判断直线
,判断直线![]() 是否过定点,若是,求出这个定点,否则说明理由.
是否过定点,若是,求出这个定点,否则说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: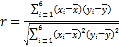 ,
,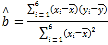
查看答案和解析>>
科目: 来源: 题型:
【题目】根据新高考改革方案,某地高考由文理分科考试变为“3+3”模式考试.某学校为了解高一年425名学生选课情况,在高一年下学期进行模拟选课,统计得到选课组合排名前4种如下表所示,其中物理、化学、生物为理科,政治、历史、地理为文科,“√”表示选择该科,“×”表示未选择该科,根据统计数据,下列判断错误的是
学科 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 |
124 | √ | √ | × | × | × | √ |
101 | × | × | √ | × | √ | √ |
86 | × | √ | √ | × | × | √ |
74 | √ | × | √ | × | √ | × |
A. 前4种组合中,选择生物学科的学生更倾向选择两理一文组合
B. 前4种组合中,选择两理一文的人数多于选择两文一理的人数
C. 整个高一年段,选择地理学科的人数多于选择其他任一学科的人数
D. 整个高一年段,选择物理学科的人数多于选择生物学科的人数
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为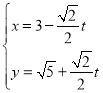 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产某种产品,一条流水线年产量为![]() 件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
第一段生产的半成品质量指标 |
|
|
|
第二段生产的成品为一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生产的成品为二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生产的成品为三等品概率 | 0.5 | 0.3 | 0.1 |
从第一道生产工序抽样调查了![]() 件,得到频率分布直方图如图:
件,得到频率分布直方图如图:

若生产一件一等品、二等品、三等品的利润分别是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各组的中间值估计为该组半成品的质量指标,估算流水线第一段生产的半成品质量指标的平均值;
(Ⅱ)将频率估计为概率,试估算一条流水线一年能为该公司创造的利润;
(Ⅲ)现在市面上有一种设备可以安装到流水线第一段,价格是![]() 万元,使用寿命是
万元,使用寿命是![]() 年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布
年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布![]() ,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
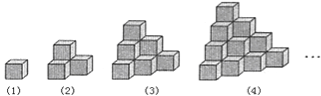
【题目】如图都是由边长为1的正方体叠成的几何体,例如第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位.依此规律,则第![]() 个几何体的表面积是__________个平方单位.
个几何体的表面积是__________个平方单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com