
科目: 来源: 题型:
【题目】给定一个数列![]() ,在这个数列里,任取
,在这个数列里,任取![]() 项,并且不改变它们在数列
项,并且不改变它们在数列![]() 中的先后次序,得到的数列称为数列
中的先后次序,得到的数列称为数列![]() 的一个
的一个![]() 阶子数列.
阶子数列.
已知数列![]() 的通项公式为
的通项公式为![]() (
(![]() 为常数),等差数列
为常数),等差数列![]() 是
是
数列![]() 的一个3阶子数列.
的一个3阶子数列.
(1)求![]() 的值;
的值;
(2)等差数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,且
阶子数列,且
![]() (
(![]() 为常数,
为常数,![]() ,求证:
,求证:![]() ;
;
(3)等比数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,
阶子数列,
求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() ,
,![]() 是直线
是直线![]() 上一动点.
上一动点.
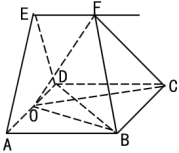
(1)求证:![]() ;
;
(2)若直线![]() 上存在唯一一点
上存在唯一一点![]() 使得直线
使得直线![]() 与平面
与平面![]() 垂直,求此时二面角
垂直,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产了![]() 两种产品投放市场,计划每年对这两种产品托人200万元,每种产品一年至少投入20万元,其中
两种产品投放市场,计划每年对这两种产品托人200万元,每种产品一年至少投入20万元,其中![]() 产品的年收益
产品的年收益![]() ,
,![]() 产品的年收益
产品的年收益![]() 与投入
与投入![]() (单位万元)分别满足
(单位万元)分别满足![]() ;若公司有100名销售人员,按照对两种产品的销售业绩分为普销售、中级销售以及金牌销售,其中普销售28人,中级销售60人,金牌销售12人
;若公司有100名销售人员,按照对两种产品的销售业绩分为普销售、中级销售以及金牌销售,其中普销售28人,中级销售60人,金牌销售12人
(1)为了使![]() 两种产品的总收益之和最大,求
两种产品的总收益之和最大,求![]() 产品每年的投入
产品每年的投入
(2)为了对表现良好的销售人员进行奖励,公司制定了两种奖励方案:
方案一:按分层抽样从三类销售中总共抽取25人给予奖励:普通销售奖励2300元,中级销售奖励5000元;金牌销售奖励8000元
方案二:每位销售都参加摸奖游戏,游戏规则:从一个装有3个白球,2个红球(求只有颜色不同)的箱子中,有放回地莫三次球,每次只能摸一只球.若摸到红球的总数为2,则可奖励1500元,若摸到红球总数是3,则可获得奖励3000元,其他情况不给予奖励,规定普通销售均可参加1次摸奖游戏;中级销售均可参加2次摸奖游戏,金牌销售均可参加3次摸奖游戏(每次摸奖的结果相互独立,奖励叠加)
(ⅰ)求方案一奖励的总金额;
(ⅱ)假设你是企业老板,试通过计算并结合实际说明,你会选择哪种方案奖励销售员.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为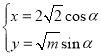 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴为非负半轴建立极坐标系,直线
轴为非负半轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
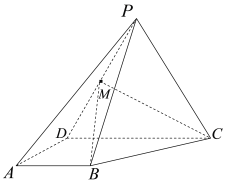
【题目】如图,在四棱锥![]() 中,等边三角形
中,等边三角形![]() 所在的平面垂直于底面
所在的平面垂直于底面![]() ,
,![]() ,
, ![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断直线![]() 与平面
与平面![]() 的是否平行,并说明理由.
的是否平行,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com