
科目: 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且满足
,且满足![]() .
.
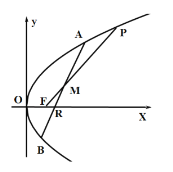
(1)若直线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】三国时期著名的数学家刘徽对推导特殊数列的求和公式很感兴趣,创造并发展了许多算法,展现了聪明才智.他在《九章算术》“盈不足”章的第19题的注文中给出了一个特殊数列的求和公式.这个题的大意是:一匹良马和一匹驽马由长安出发至齐地,长安与齐地相距3000里(1里=500米),良马第一天走193里,以后每天比前一天多走13里.驽马第一天走97里,以后每天比前一天少走半里.良马先到齐地后,马上返回长安迎驽马,问两匹马在第几天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,若
,若![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.当![]() 时,数列
时,数列![]() 是有穷数列B.当
是有穷数列B.当![]() 时,数列
时,数列![]() 是有穷数列
是有穷数列
C.当数列![]() 是无穷数列时,数列
是无穷数列时,数列![]() 单调D.当数列
单调D.当数列![]() 单调时,数列
单调时,数列![]() 是无穷数列
是无穷数列
查看答案和解析>>
科目: 来源: 题型:
【题目】2021年我省将实施新高考,新高考“依据统一高考成绩、高中学业水平考试成绩,参考高中学生综合素质评价信息”进行人才选拔。我校2018级高一年级一个学习兴趣小组进行社会实践活动,决定对某商场销售的商品A进行市场销售量调研,通过对该商品一个阶段的调研得知,发现该商品每日的销售量![]() (单位:百件)与销售价格
(单位:百件)与销售价格![]() (元/件)近似满足关系式
(元/件)近似满足关系式![]() ,其中
,其中![]() 为常数
为常数![]() 已知销售价格为3元/件时,每日可售出该商品10百件。
已知销售价格为3元/件时,每日可售出该商品10百件。
(1)求函数![]() 的解析式;
的解析式;
(2)若该商品A的成本为2元/件,根据调研结果请你试确定该商品销售价格的值,使该商场每日销售该商品所获得的利润(单位:百元)最大。
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. “![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”
”
D. “若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题
”的逆命题为真命题
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面四边形![]() 中,
中,![]() ,
,![]() ,再将
,再将![]() 沿着
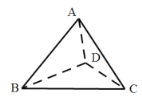
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角,设二面角
所成角,设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.存在
C.存在![]() D.存在
D.存在![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com