
科目: 来源: 题型:
【题目】动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦
轴上截得的弦![]() 的长为4.
的长为4.
(1)若动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)在曲线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使过点
,使过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 满足
满足![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将斜边长为![]() 的等腰直角
的等腰直角![]() 沿斜边
沿斜边![]() 上的高
上的高![]() 折成直二面角
折成直二面角![]() ,
,![]() 为
为![]() 中点.
中点.
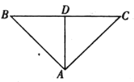
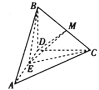
(1)求二面角![]() 的余弦值;
的余弦值;
(2)![]() 为线段
为线段![]() 上一动点,当直线
上一动点,当直线![]() 与平面
与平面![]() 所成的角最大时,求三棱锥
所成的角最大时,求三棱锥![]() 外接球的体积.
外接球的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了了解该市教师年龄分布情况,对年龄在![]() 内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
年龄区间 |
|
|
|
|
教师人数 | 2000 | 1300 | ||
样本人数 | 130 |
由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在![]() 的样本人数比年龄在
的样本人数比年龄在![]() 的样本人数多10,根据以上信息回答下列问题:
的样本人数多10,根据以上信息回答下列问题:

(1)求该市年龄在![]() 的教师人数;
的教师人数;
(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数![]() 及方差
及方差![]() (同一组的数据用该组区间的中点值作代表).
(同一组的数据用该组区间的中点值作代表).
查看答案和解析>>
科目: 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了人口规模相当的![]() 个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价:
个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价: ![]() (单位:元/月)和购买总人数
(单位:元/月)和购买总人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
定价x(元/月) | 20 | 30 | 50 | 60 |
年轻人(40岁以下) | 10 | 15 | 7 | 8 |
中老年人(40岁以及40岁以上) | 20 | 15 | 3 | 2 |
购买总人数y(万人) | 30 | 30 | 10 | 10 |
(Ⅰ)根据表中的数据,请用线性回归模型拟合![]() 与
与![]() 的关系,求出
的关系,求出![]() 关于
关于![]() 的回归方程;并估计
的回归方程;并估计![]() 元/月的流量包将有多少人购买?
元/月的流量包将有多少人购买?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包称为低价流量包,
元)的流量包称为低价流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过
元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过![]() 的前提下,认为购买人的年龄大小与流量包价格高低有关?
的前提下,认为购买人的年龄大小与流量包价格高低有关?
定价x(元/月) | 小于50元 | 大于或等于50元 | 总计 |
年轻人(40岁以下) | |||
中老年人(40岁以及40岁以上) | |||
总计 |
参考公式:其中![]()
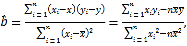
![]()
![]() 其中
其中![]()
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
查看答案和解析>>
科目: 来源: 题型:
【题目】港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
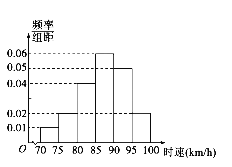
A. 300,![]() B. 300,
B. 300,![]() C. 60,
C. 60,![]() D. 60,
D. 60,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线斜率为0.函数
处的切线斜率为0.函数![]()
(1)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 的单调区间;
的单调区间;
(3)令![]() ,设函数
,设函数![]() 在
在![]()
![]() 处取得极值,记点
处取得极值,记点![]() ,
,![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() ,
,![]() 的公共点.
的公共点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,
两点,![]() 都在
都在![]() 轴上方,并且
轴上方,并且![]() 在
在![]() 之间,且
之间,且![]() 到直线
到直线![]() 的距离是
的距离是![]() 到直线
到直线![]() 距离的
距离的![]() 倍.
倍.
①记![]() 的面积分别为
的面积分别为![]() ,求
,求![]() ;
;
②若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com