
科目: 来源: 题型:
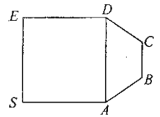
【题目】某产品的包装纸可类比如图所示的平面图形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包装的过程中,沿着
,在包装的过程中,沿着![]() 将正方形
将正方形![]() 折起,直至
折起,直至![]() ,得到多面体
,得到多面体![]() ,
,![]() 分别为
分别为![]() 中点.
中点.
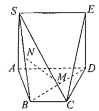
(1)证明:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】阳马和鳖臑(bienao)是《九章算术·商功》里对两种锥体的称谓.如图所示,取一个长方体,按下图斜割一分为二,得两个模一样的三棱柱,称为堑堵(如图).再沿其中一个堑堵的一个顶点与相对的棱剖开,得四棱锥和三棱锥各一个,有一棱与底面垂直的四棱锥称为阳马(四棱锥![]() )余下三棱锥称为鳖臑(三棱锥
)余下三棱锥称为鳖臑(三棱锥![]() )若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )
)若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以轴正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 分别交于异于极点O的四点A,B,C,D.
分别交于异于极点O的四点A,B,C,D.
(1)若曲线![]() 关于
关于![]() 对称,求
对称,求![]() 的值,并求
的值,并求![]() 的参数方程;
的参数方程;
(2)若![]() |,当
|,当![]() 时,求
时,求![]() 的范围.
的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的左右焦点分别为F1,F2,点
的左右焦点分别为F1,F2,点![]() 在椭圆C上,满足
在椭圆C上,满足![]() .
.
(1)求椭圆C的标准方程;
(2)直线l1过点P,且与椭圆只有一个公共点,直线l2与l1的倾斜角互补,且与椭圆交于异于点P的两点M,N,与直线x=1交于点K(K介于M,N两点之间).
①问:直线PM与PN的斜率之和能否为定值,若能,求出定值并写出详细计算过程;若不能,请说明理由;
②求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: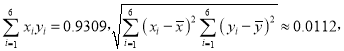
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,已知PA⊥平面ABCD,△ABC为等边三角形,PA=2AB=2,AC⊥CD,PD与平面PAC所成角的余弦值为![]() .
.
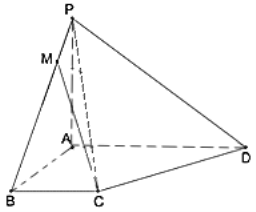
(1)证明:![]() 平面PAD;
平面PAD;
(2)点M为PB上一点,且![]() ,试判断点M的位置.
,试判断点M的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】直角坐标系xOy中,已知MN是圆C:(x﹣2)2+(y﹣3)2=2的一条弦,且CM⊥CN,P是MN的中点.当弦MN在圆C上运动时,直线l:x﹣y﹣5=0上总存在两点A,B,使得![]() 恒成立,则线段AB长度的最小值是_____.
恒成立,则线段AB长度的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com