
科目: 来源: 题型:
【题目】针对时下的“抖音热”某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() ,若有
,若有![]() 的把握认为是否喜欢抖音和性别有关则调查人数中男生可能有( )人
的把握认为是否喜欢抖音和性别有关则调查人数中男生可能有( )人
附表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附:
A.20B.40C.60D.80
查看答案和解析>>
科目: 来源: 题型:
【题目】春节期间爆发的新型冠状病毒(COVID-19)是新中国成立以来感染人数最多的一次疫情.一个不知道自己已感染但处于潜伏期的甲从疫区回到某市过春节,回到家乡后与朋友乙、丙、丁相聚过,最终乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的,丙是受甲或乙感染的,假设他受甲和受乙感染的概率分别是![]() 和
和![]() .丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是
.丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是![]() 、
、![]() 和
和![]() .在这种假设之下,乙、丙、丁中直接受甲感染的人数为
.在这种假设之下,乙、丙、丁中直接受甲感染的人数为![]() .
.
(1)求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)该市在发现在本地出现新冠病毒感染者后,迅速采取应急措施,其中一项措施是各区必须每天及时,上报新增疑似病例人数.![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,中位数
,中位数![]() ”,
”,![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,总体方差为
,总体方差为![]() ”.设
”.设![]() 区和
区和![]() 区连续
区连续![]() 天上报新增疑似病例人数分别为
天上报新增疑似病例人数分别为![]() 和
和![]() ,
,![]() 和
和![]() 分别表示
分别表示![]() 区和
区和![]() 区第
区第![]() 天上报新增疑似病例人数(
天上报新增疑似病例人数(![]() 和
和![]() 均为非负).记
均为非负).记![]() ,
,![]() .
.
①试比较![]() 和
和![]() 的大小;
的大小;
②求![]() 和
和![]() 中较小的那个字母所对应的
中较小的那个字母所对应的![]() 个数有多少组?
个数有多少组?
查看答案和解析>>
科目: 来源: 题型:
【题目】设点![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 、
、![]() 是
是![]() 上两点.若
上两点.若![]() ,且线段
,且线段![]() 的中点到
的中点到![]() 轴的距离等于
轴的距离等于![]() .
.
(1)求![]() 的值;
的值;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点且在
两点且在![]() 轴的截距为负,过
轴的截距为负,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() .
.
(i)证明:直线![]() 恒过定点,并求出该定点的坐标;
恒过定点,并求出该定点的坐标;
(ii)求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l的参数方程为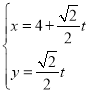 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当 ![]() 时,求函数
时,求函数![]() 图象在点
图象在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)是否存在实数![]() ,对任意
,对任意![]() ,
,![]() 且
且![]() 有
有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 周长为8.
周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() ,使以
,使以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,若存在求出直线
,若存在求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出5人,进行体育锻炼体会交流,从参加体会交流的5人中,随机选出2人作重点发言,求恰好选出一名男生的概率.
参考公式: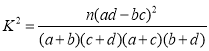 ,其中
,其中![]()
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com