
科目: 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


查看答案和解析>>
科目: 来源: 题型:
【题目】2020年席卷全球的新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早诊断、早隔离、早治疗是有效防控疾病蔓延的重要举措之一.某社区对![]() 位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为
位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为![]() %,且每个人的口拭子核酸是否呈阳性相互独立.
%,且每个人的口拭子核酸是否呈阳性相互独立.
(1)假设该疾病患病的概率是![]() %,且患病者口拭子核酸呈阳性的概率为
%,且患病者口拭子核酸呈阳性的概率为![]() %,设这
%,设这![]() 位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)根据经验,口拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将![]() 位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
方案二:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
试分析哪一个方案的工作量更少?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,记
,记![]() ,
,![]() ,若同时满足条件①
,若同时满足条件①![]() ,
,![]() 均单调递增;②
均单调递增;②![]() 且
且![]() ,则称
,则称![]() ,
,![]() 是无穷互补数列.
是无穷互补数列.
(1)若![]() ,
,![]() ,试判断数列
,试判断数列![]() ,
,![]() 是否为无穷互补数列,并说明理由;
是否为无穷互补数列,并说明理由;
(2)若![]() ,且
,且![]() ,
,![]() 是无穷互补数列,求数列
是无穷互补数列,求数列![]() 前
前![]() 项的和.
项的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 过点
过点![]() ,且与
,且与![]() 内切,设
内切,设![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() ,
,
(1)求轨迹C的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,判断直线
,判断直线![]() 是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在边长为2的等边![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,将AED沿
的中点,将AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如图2的四棱锥A-BCDE,连结
,得到如图2的四棱锥A-BCDE,连结![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
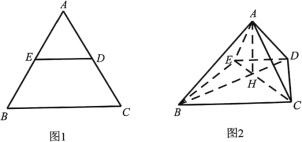
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着马拉松运动在全国各地逐渐兴起,参与马拉松训练与比赛的人数逐年增加.为此,某市对参加马拉松运动的情况进行了统计调査,其中一项是调査人员从参与马拉松运动的人中随机抽取100人,对其每月参与马拉松运动训练的夭数进行统计,得到以下统计表;
平均每月进行训练的天数 |
|
|
|
人数 | 15 | 60 | 25 |
(1)以这100人平均每月进行训练的天数位于各区间的频率代替该市参与马拉松训练的人平均每月进行训练的天数位于该区间的概率.从该市所有参与马拉松训练的人中随机抽取4个人,求恰好有2个人是“平均每月进行训练的天数不少于20天”的概率;
(2)依据统计表,用分层抽样的方法从这100个人中抽取12个,再从抽取的12个人中随机抽取3个,![]() 表示抽取的是“平均每月进行训练的天数不少于20天”的人数,求
表示抽取的是“平均每月进行训练的天数不少于20天”的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类:可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由10位同学组成四个宣传小组,其中可回收物与餐厨垃圾宣传小组各有2位同学,有害垃圾与其他垃圾宣传小组各有3位同学.现从这10位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 与直线
与直线![]() 的两个交点之间的距离;
的两个交点之间的距离;
(2)若曲线![]() 上的点到直线
上的点到直线![]() 距离的最大值为
距离的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com