
科目: 来源: 题型:
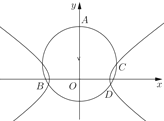
【题目】如图,已知圆![]() :
:![]() (
(![]() )和双曲线
)和双曲线![]() :
:![]() (
(![]() ),记
),记![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴负半轴的公共点分别为
轴负半轴的公共点分别为![]() 、
、![]() ,又记
,又记![]() 与
与![]() 在第一、第四象限的公共点分别为
在第一、第四象限的公共点分别为![]() 、
、![]() .
.
(1)若![]() ,且
,且![]() 恰为
恰为![]() 的左焦点,求
的左焦点,求![]() 的两条渐近线的方程;
的两条渐近线的方程;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 恰为
恰为![]() 的左焦点,求证:在
的左焦点,求证:在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目: 来源: 题型:
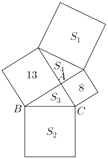
【题目】某市计划在一片空地上建一个集购物、餐饮、娱乐为一体的大型综合园区,如图,已知两个购物广场的占地都呈正方形,它们的面积分别为13公顷和8公顷;美食城和欢乐大世界的占地也都呈正方形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为
公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷.
公顷.
(1)设![]() ,用关于
,用关于![]() 的函数
的函数![]() 表示
表示![]() ,并求
,并求![]() 在区间
在区间![]() 上的最大值的近似值(精确到0.001公顷);
上的最大值的近似值(精确到0.001公顷);
(2)如果![]() ,并且
,并且![]() ,试分别求出
,试分别求出![]() 、
、![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若![]() 是递增数列,数列
是递增数列,数列![]() 满足:对任意
满足:对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则称
,则称![]() 是
是![]() 的“分隔数列”.
的“分隔数列”.
(1)设![]() ,证明:数列
,证明:数列![]() 是
是![]() 的分隔数列;
的分隔数列;
(2)设![]() 是
是![]() 的前n项和,
的前n项和,![]() ,判断数列
,判断数列![]() 是否是数列
是否是数列![]() 的分隔数列,并说明理由;
的分隔数列,并说明理由;
(3)设![]() 是
是![]() 的前n项和,若数列
的前n项和,若数列![]() 是
是![]() 的分隔数列,求实数
的分隔数列,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
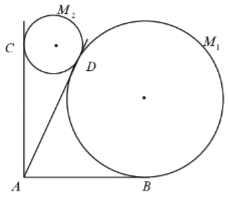
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.

(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )若过点
)若过点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相交于点
相交于点![]() ,试判断点
,试判断点![]() 是否在定直线上?若是,请求出定直线的方程;若不是,请说明理由.
是否在定直线上?若是,请求出定直线的方程;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某试点城市环保局从该市市区2015年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)

(1)求中位数.
(2)从这15天的数据中任取两天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列及数学期望.
(3)以这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com