
科目: 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
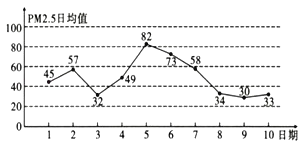
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:
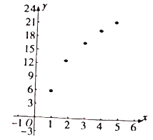
(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中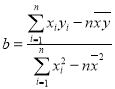 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知动圆![]() 过点
过点![]() ,且在
,且在![]() 轴上截得弦
轴上截得弦![]() 的长为4.
的长为4.

(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() ,过点
,过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与轨迹
分别与轨迹![]() 交于
交于![]() ,
,![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试问
,试问![]() 是否为定值?若是,求出此定值;若不是,请说明理由.
是否为定值?若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为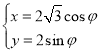 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
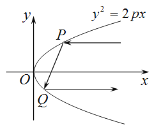
【题目】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.现有抛物线![]() ,如图一平行于
,如图一平行于![]() 轴的光线射向抛物线,经两次反射后沿平行
轴的光线射向抛物线,经两次反射后沿平行![]() 轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示,根据图表,下面叙述不正确的是( )
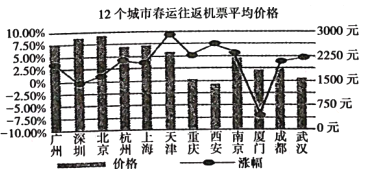
A. 同去年相比,深圳的变化幅度最小且厦门的平均价格有所上升
B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高
C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州
D. 同去年相比,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他门各应偿还多少?该问题中,1斗为10升,则羊主人应偿还多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s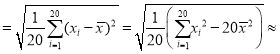 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com