【题目】已知各项均为正数的数列的前n项和为，.

（1）求数列的通项公式；

（2）记，若集合中恰好有3个元素，求实数的取值范围；

（3）若，且，求证：数列为等差数列.

【题目】如图，已知椭圆C：的左、右顶点分别为右焦点为，右准线l的方程为，过焦点F的直线与椭圆C相交于点A，B（不与点重合）.

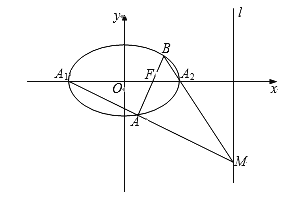
（1）求椭圆C的标准方程；

（2）当直线AB的倾斜角为45°时，求弦AB的长；

（3）设直线交l于点M，求证：B，，M三点共线.

【题目】如图，在四棱锥P-ABCD中，已知四边形ABCD是边长为2的正方形，平面ABCD，E是棱PB的中点，且过AE和AD的平面与棱PC交于点F.

（1）求证：；

（2）若平面平面PBC，求线段PA的长.

【题目】如图，已知椭圆的左右顶点分别是，离心率为，设点，连接交椭圆于点，坐标原点是．

（1）证明： ；

（2）设三角形的面积为，四边形的面积为， 若 的最小值为1，求椭圆的标准方程．

【题目】如图,在四棱锥中, 平面平面,.

（1）求证:平面；

（2）求直线与平面所成角的正弦值；

（3）在棱上是否存在点,使得平面？若存在, 求的值；若不存在, 说明理由.

已知函数=|x-a|+(a≠0)

(1)若不等式-≤1恒成立,求实数m的最大值;

(2)当a<时,函数g(x)=+|2x-1|有零点,求实数a的取值范围

【题目】跨年迎新联欢晚会简称跨年晚会，是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动，跨年晚会首次出现在港台地区，跨年晚会因形式和举办地不同因而名称也不同，如央视启航2020跨年盛典，湖南卫视跨年演唱会，东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度，现分别随机选出名观众对迎新晚会的质量评估评分，最高分为分，综合得分情况如下表所示：

根据表中的数据，回答下列问题：

（1）根据表中的数据，绘制这位观众打分的频率分布直方图；

（2）已知观众的评分近似服从，其中是反应随机变量取值的平均水平的特征数，工作人员在分析数据时发现，可用位观众评分的平均数估计，但由于评分观众人数较少，误差较大，所以不能直接用位观众评分的标准差的值估计，而在这位观众打分的频率分布直方图的基础上依据来估计更科学合理，试求和的估计值（的结果精确到小数点后两位）.

【题目】我国古代有辉煌的数学研究成果，其中《周髀算经》，《九章算术》，《海岛算经》，《孙子算经》，《缉古算经》均有着十分丰富的内容，是了解我国古代数学的重要文献，某中学计划将这本专著作为高中阶段“数学文化”样本课程选修内容，要求每学年至少选一科，三学年必须将门选完，则小南同学的不同选修方式有______种.

【题目】在无穷数列中，，且，记的前n项和为.

（1）若，求的值；

（2）若，求的值；

（3）证明：中必有一项为1或3.

【题目】在平面直角坐标系中，的顶点，，且、、成等差数列.

（1）求的顶点的轨迹方程；

（2）直线与顶点的轨迹交于两点，当线段的中点落在直线上时，试问：线段的垂直平分线是否恒过定点？若过定点，求出定点的坐标；若不过定点，请说明理由.