【题目】已知，，有如下结论：

①有两个极值点；

②有个零点；

③的所有零点之和等于零.

则正确结论的个数是（ ）

A.B.C.D.

【题目】人口平均预期寿命是综合反映人们健康水平的基本指标.年第六次全国人口普查资料表明，随着我国社会经济的快速发展，人民生活水平的不断提高以及医疗卫生保障体系的逐步完善，我国人口平均预期寿命继续延长，国民整体健康水平有较大幅度的提高.下图体现了我国平均预期寿命变化情况，依据此图，下列结论错误的是（ ）

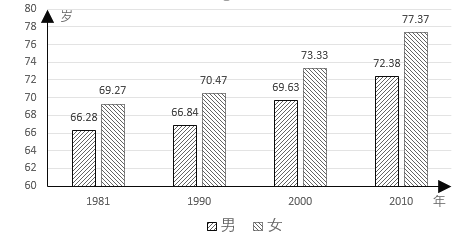
A.男性的平均预期寿命逐渐延长

B.女性的平均预期寿命逐渐延长

C.男性的平均预期寿命延长幅度略高于女性

D.女性的平均预期寿命延长幅度略高于男性

【题目】已知为正整数，各项均为正整数的数列满足：，记数列的前项和为．

（1）若，求的值；

（2）若，求的值；

（3）若为奇数，求证：“”的充要条件是“为奇数”．

【题目】已知椭圆过点，且它的一个焦点与抛物线的焦点相同．直线过点，且与椭圆相交于两点．

（1）求椭圆的方程；

（2）若直线的一个方向向量为，求的面积（其中为坐标原点）；

（3）试问：在轴上是否存在点，使得为定值？若存在，求出点的坐标和定值；若不存在，请说明理由．

【题目】某村共有100户农民，且都从事蔬菜种植，平均每户的年收入为2万元．为了调整产业结构，该镇政府决定动员部分农民从事蔬菜加工．据估计，若能动员户农民从事蔬菜加工，则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高，而从事蔬菜加工的农民平均每户的年收入为万元．

（1）在动员户农民从事蔬菜加工后，要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入，求的取值范围；

（2）在（1）的条件下，要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入，求的最大值．

【题目】已知数列{an}满足．

（1）求a1，a2，a3的值；

（2）对任意正整数n，an小数点后第一位数字是多少？请说明理由．

（Ⅰ）理论上，小球落入4号容器的概率是多少？

（Ⅱ）一数学兴趣小组取3个小球进行试验，设其中落入4号容器的小球个数为，求的分布列与数学期望.

【题目】已知正项数列中，，点在抛物线上.数列中，点在经过点，以为方向向量的直线上.

（1）求数列，的通项公式；

（2）若，问是否存在，使得成立？若存在，求出的值；若不存在，说明理由；

（3）对任意的正整数，不等式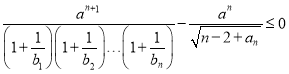成立，求正数的取值范围.

【题目】某小区内有一块以为圆心半径为20米的圆形区域.广场，为丰富市民的业余文化生活，现提出如下设计方案：如图，在圆形区域内搭建露天舞台，舞台为扇形区域，其中两个端点，分别在圆周上；观众席为梯形内且在圆外的区域，其中，，且，在点的同侧.为保证视听效果，要求观众席内每一个观众到舞台处的距离都不超过60米.设.

（1）求的长（用表示）；

（2）对于任意，上述设计方案是否均能符合要求？

【题目】已知函数，且存在，使得，设，，，．

（Ⅰ）证明单调递增；

（Ⅱ）求证：；

（Ⅲ）记，其前项和为，求证：．