
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点为
)的右顶点为![]() .左、右焦点分别为
.左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆于点
轴的直线交椭圆于点![]() (
(![]() 在第象限),直线
在第象限),直线![]() 的斜率为
的斜率为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不与
不与![]() 、
、![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
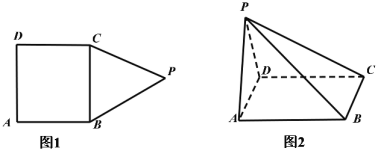
【题目】如图,在多边形![]() 中(图1).四边形
中(图1).四边形![]() 为长方形,
为长方形,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,现以
,现以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 内的射影恰好是
内的射影恰好是![]() 的中点(图2).
的中点(图2).
(1)证明:![]() 平面
平面![]() :
:
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
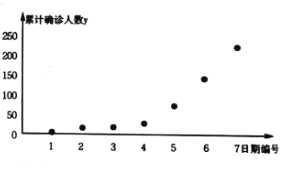
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为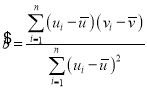 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点为
)的右顶点为![]() .左、右焦点分别为
.左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆于点
轴的直线交椭圆于点![]() (
(![]() 在第象限),直线
在第象限),直线![]() 的斜率为
的斜率为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不与
不与![]() 、
、![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
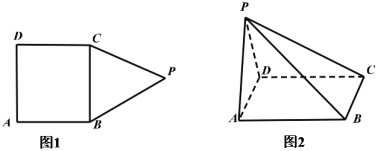
【题目】如图,在多边形![]() 中(图1).四边形
中(图1).四边形![]() 为长方形,
为长方形,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,现以
,现以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 内的射影恰好是
内的射影恰好是![]() 的中点(图2).
的中点(图2).
(1)证明:![]() 平面
平面![]() :
:
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
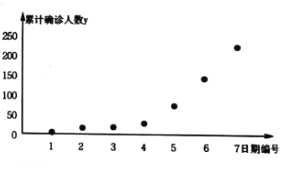
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为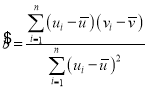 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com