
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
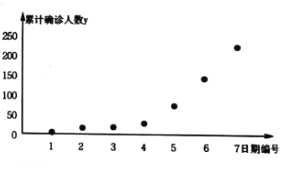
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为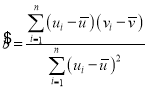 ,
,![]() .
.
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
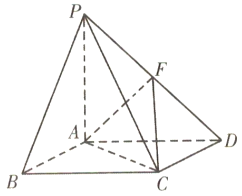
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多边形![]() 中(图1).四边形
中(图1).四边形![]() 为长方形,
为长方形,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,现以
,现以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 内的射影恰好是
内的射影恰好是![]() 的中点(图2).
的中点(图2).
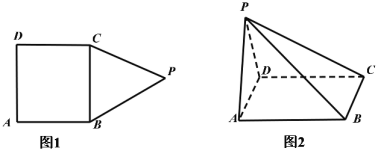
(1)证明:![]() 平面
平面![]() :
:
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们通常以分贝(符号是![]() )为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为
)为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为![]() 的声音对应的等级为
的声音对应的等级为![]() ,则有
,则有![]() ,则
,则![]() 的声音与
的声音与![]() 的声音强度之比为( )
的声音强度之比为( )
A.10B.100C.1000D.10000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如图所示:
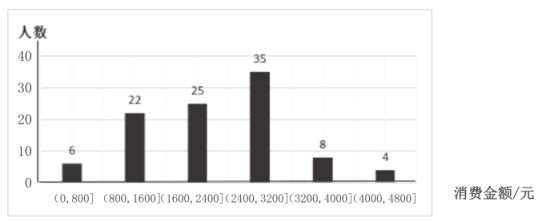
(1)现从去年的消费金额超过3200元的消费者中随机抽取2人,求至少有1位消费者,其去年的消费者金额在![]() 的范围内的概率;
的范围内的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
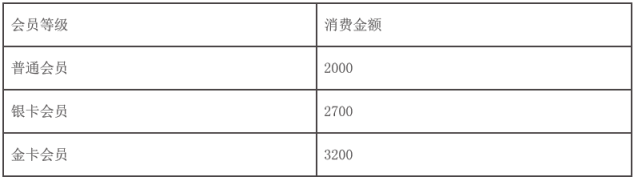
预计去年消费金额在![]() 内的消费者今年都将会申请办理普通会员,消费金额在
内的消费者今年都将会申请办理普通会员,消费金额在![]() 内的消费者都将会申请办理银卡会员,消费金额在
内的消费者都将会申请办理银卡会员,消费金额在![]() 内的消费者都将会申请办理金卡会员,消费者在申请办理会员时,需一次性缴清相应等级的消费金额,该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
内的消费者都将会申请办理金卡会员,消费者在申请办理会员时,需一次性缴清相应等级的消费金额,该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励:
普通会员中的“幸运之星”每人奖励500元;银卡会员中的“幸运之星”每人奖励600元;金卡会员中的“幸运之星”每人奖励800元.
方案二:每位会员均可参加摸奖游戏,游戏规则如下:从一个装有3个白球、2个红球(球只有颜色不同)的箱子中,有放回地摸三次球,每次只能摸一个球,若摸到红球的总数为2,则可获得200元奖励金;若摸到红球的总数为3,则可获得300元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加1次摸奖游戏;每位银卡会员均可参加2次摸奖游戏;每位金卡会员均可参加3次摸奖游戏(每次摸奖的结果相互独立)
请你预测哪一种返利活动方案该健身机构的投资较少?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com