
科目: 来源: 题型:
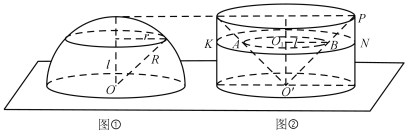
【题目】祖暅原理指出:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等,例如在计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某地一条主于道上有46盏路灯,相邻两盏路灯之间间隔30米,有关部门想在所有相邻路灯间都新添一盏,假设工人每次在两盏灯之间添新路灯是随机,并且每次添新路灯相互独立.新添路灯与左右相邻路灯的间隔都不小于10米是符合要求的,记符合要求的新添路灯数量为![]() ,则
,则![]() ( )
( )
A.30B.15C.10D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为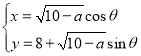 (
(![]() 为参数,常数
为参数,常数![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 及直线
及直线![]() 的直角坐标方程,并指出
的直角坐标方程,并指出![]() 是什么曲线;
是什么曲线;
(2)设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作两条相互垂直的直线
分别作两条相互垂直的直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 的交点为
的交点为![]() ,三角形
,三角形![]() 面积的最大值为1.
面积的最大值为1.
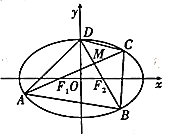
(1)求椭圆![]() 的方程;
的方程;
(2)当四边形![]() 的面积
的面积![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解市民对电视剧市场的爱好,某上星电视台邀请了100位电视剧爱好者(男50人、女50人)对4月份观看其播出的电视剧集数进行调研,得到这100名电视剧爱好者观看集数的中位数为39集(假设这100名电视剧爱好者的观看集数均在![]() 集内),且观看集数在
集内),且观看集数在![]() 集内的人数为15,并根据调查结果画出如图所示的频率分布直方图.
集内的人数为15,并根据调查结果画出如图所示的频率分布直方图.

(1)求![]() ,
,![]() 的值;
的值;
(2)有些观众喜欢带有主角光环意识来观剧.但是最近几年的影视作品里出现了一个有趣的趋势——攻气十足的女性角色越来越讨人喜欢,傻白甜的女主们则破了主角光环,各种被嫌弃,更有些剧集中明明是女配的脚本,却因为更具有大女主气场,而获得了比主角更多的关注与声量,如《完美关系》里的斯黛拉,《精英律师》里的栗娜,《我的前半生》里的唐晶,……已知在这100名电视剧爱好者的女性中有31名认为自己有主角光环意识,男性中有19名认为自己有主角光环意识,根据以上数据请同学们制作出列联表,并且判断能否在犯错误的概率不超过0.001的前提下认为性别与是否观剧带有主角光环意识有关系?
参考公式及数据: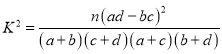 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
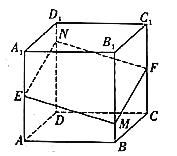
【题目】如图,已知多面体![]() 是正方体,
是正方体,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面与棱
的平面与棱![]() 交于点
交于点![]() ,则以下说法不正确的是( )
,则以下说法不正确的是( )
A.四边形![]() 是平行四边形
是平行四边形
B.四边形![]() 是菱形
是菱形
C.当点![]() 从点
从点![]() 往点
往点![]() 运动时,四边形
运动时,四边形![]() 的面积先增大后减小
的面积先增大后减小
D.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积一直增大
的体积一直增大
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年泉州市农村电商发展迅猛,成为创新农产品交易方式、增加农民收入、引导农业供给侧结构性改革、促进乡村振兴的重要力量,成为乡村振兴的新引擎.2019年大学毕业的李想,选择回到家乡泉州自主创业,他在网上开了一家水果网店.2019年双十一期间,为了增加水果销量,李想设计了下面两种促销方案:方案一:购买金额每满120元,即可抽奖一次,中奖可获得20元,每次中奖的概率为![]() (
(![]() ),假设每次抽奖相互独立.方案二:购买金额不低于180元时,即可优惠
),假设每次抽奖相互独立.方案二:购买金额不低于180元时,即可优惠![]() 元,并在优惠后的基础上打九折.
元,并在优惠后的基础上打九折.
(1)在促销方案一中,设每10个抽奖人次中恰有6人次中奖的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() ;
;
(2)若促销方案二中,李想每笔订单得到的金额均不低于促销前总价的八折,求![]() 的最大值;
的最大值;
(3)以(1)中确定的![]() 作为
作为![]() 的值,且当
的值,且当![]() 取最大值时,若某位顾客一次性购买了360元,则该顾客应选择哪种促销方案?请说明理由.
取最大值时,若某位顾客一次性购买了360元,则该顾客应选择哪种促销方案?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com