
科目: 来源: 题型:
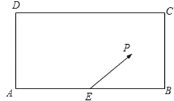
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
查看答案和解析>>
科目: 来源: 题型:
【题目】某景区提供自行车出租,该景区有辆自行车供游客租赁使用,管理这些自行车的费用是每日![]() 元.根据经验,若每辆自行车的日租金不超过
元.根据经验,若每辆自行车的日租金不超过![]() 元,则自行车可以全部租出;若超出
元,则自行车可以全部租出;若超出![]() 元,则每超过
元,则每超过![]() 元,租不出的自行车就增加
元,租不出的自行车就增加![]() 辆.为了便于结算,每辆自行车的日租金
辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(1)求函数![]() 的解析式;
的解析式;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 与
与![]() 在给定的区间上满足
在给定的区间上满足![]() 恒成立,则称这两个函数在该区间上“和谐”。
恒成立,则称这两个函数在该区间上“和谐”。
(1)若函数![]() 与
与![]() 在R上和谐,求实数a的取值范围;
在R上和谐,求实数a的取值范围;
(2)若函数![]() 与
与![]() 在
在![]() 上和谐,求实数a的取值范围.
上和谐,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定函数![]() 和
和![]() ,令
,令![]() ,对以下三个论断:
,对以下三个论断:
(1)若![]() 和
和![]() 都是奇函数,则
都是奇函数,则![]() 也是奇函数;(2)若
也是奇函数;(2)若![]() 和
和![]() 都是非奇非偶函数,则
都是非奇非偶函数,则![]() 也是非奇非偶函数:(3)
也是非奇非偶函数:(3)![]() 和
和![]() 之一与
之一与![]() 有相同的奇偶性;其中正确论断的个数为( )
有相同的奇偶性;其中正确论断的个数为( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com