
科目: 来源: 题型:
【题目】给定无穷数列![]() ,若无穷数列
,若无穷数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,则称
,则称![]() 与
与![]() “接近”.
“接近”.
(1)设![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() ,
,![]() ,判断数列
,判断数列![]() 是否与
是否与![]() 接近,并说明理由;
接近,并说明理由;
(2)已知![]() 是公差为
是公差为![]() 的等差数列,若存在数列
的等差数列,若存在数列![]() 满足:
满足:![]() 与
与![]() 接近,且在
接近,且在![]() 这100个值中,至少有一半是正数,求
这100个值中,至少有一半是正数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示1-9的一种方法.则据此,3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”,现有6根算筹,据此表示方法,若算筹不能剩余,则可以用1-9这9数字表示的两位数的个数为( )
”,现有6根算筹,据此表示方法,若算筹不能剩余,则可以用1-9这9数字表示的两位数的个数为( )
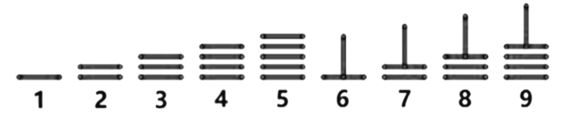
A.9B.13C.16D.18
查看答案和解析>>
科目: 来源: 题型:
【题目】等差数列的![]() 公差
公差![]() 不为0,
不为0,![]() 是其前
是其前![]() 项和,给出下列命题:
项和,给出下列命题:
①若![]() ,且
,且![]() ,则
,则![]() 和
和![]() 都是
都是![]() 中的最大项;
中的最大项;
②给定![]() ,对一切
,对一切![]() ,都有
,都有![]() ;
;
③若![]() ,则
,则![]() 中一定有最小项;
中一定有最小项;
④存在![]() ,使得
,使得![]() 和
和![]() 同号.
同号.
其中正确命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
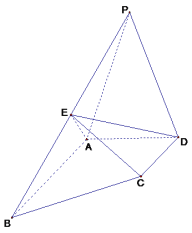
(1)求证:平面PAB⊥平面CDE;
(2)若AD=CD=2,求点P到平面ADE的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润60元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(1)若商品一天购进该商品10件,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:件,
(单位:件,![]() )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量![]() (单位:件,
(单位:件,![]() ),整理得下表:
),整理得下表:

若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中a是常数).
(其中a是常数).
(1)求过点![]() 与曲线
与曲线![]() 相切的直线方程;
相切的直线方程;
(2)是否存在![]() 的实数,使得只有唯一的正数a,当
的实数,使得只有唯一的正数a,当![]() 时不等式
时不等式![]() 恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知BD为圆锥AO底面的直径,若![]() ,C是圆锥底面所在平面内一点,
,C是圆锥底面所在平面内一点,![]() ,且AC与圆锥底面所成角的正弦值为
,且AC与圆锥底面所成角的正弦值为![]() .
.
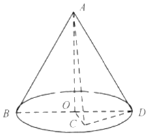
(1)求证:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com