
科目: 来源: 题型:
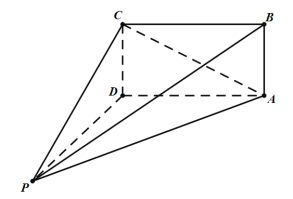
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
查看答案和解析>>
科目: 来源: 题型:
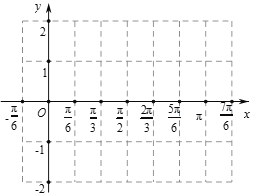
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
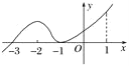
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴极坐标,曲线
轴非负半轴为极轴极坐标,曲线![]() 的方程:
的方程: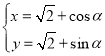 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程:
的方程: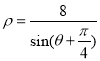 .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)从![]() 上任意一点
上任意一点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求切线长
,求切线长![]() 的最小值及此时点
的最小值及此时点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】手机支付也称为移动支付,是指允许用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.随着信息技术的发展,手机支付越来越成为人们喜欢的支付方式.某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用手机支付的人数如下所示:(年龄单位:岁)
年龄段 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
(2)若从年龄在[55,65),[65,75]的样本中各随机选取2人进行座谈,记选中的4人中“使用手机支付”的人数为X,求随机变量X的分布列和数学期望.
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为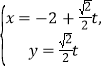 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C.扇形的周长为![]() ,则当其圆心角的弧度数为
,则当其圆心角的弧度数为![]() 时,其面积最大
时,其面积最大
D.若扇形的周长为![]() ,面积为
,面积为![]() ,则该扇形的圆心角的弧度数为
,则该扇形的圆心角的弧度数为![]() 或
或![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于正整数集合![]() ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素![]() 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“可分集合”.
为“可分集合”.
(1)判断集合![]() 和
和![]() 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);
(2)求证:五个元素的集合![]() 一定不是“可分集合”;
一定不是“可分集合”;
(3)若集合![]() 是“可分集合”.
是“可分集合”.
①证明:![]() 为奇数;
为奇数;
②求集合![]() 中元素个数的最小值.
中元素个数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com