
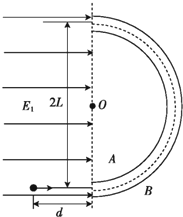
 如图所示,两块直径为2L的同心半圆形带电金属板A、B固定在竖直平面内,两板间的距离很近,可认为A、B间的电场场强大小处处相等、方向都指向圆心O.在A、B左侧有方向水平向右、场强大小为E的匀强电场.现从正对A、B板间隙、到两板的一端距离为d处由静止释放一个质量为m、电荷量为q的带正电微粒(不计重力),发现此微粒恰能在两板间运动而不与板发生相互作用.
如图所示,两块直径为2L的同心半圆形带电金属板A、B固定在竖直平面内,两板间的距离很近,可认为A、B间的电场场强大小处处相等、方向都指向圆心O.在A、B左侧有方向水平向右、场强大小为E的匀强电场.现从正对A、B板间隙、到两板的一端距离为d处由静止释放一个质量为m、电荷量为q的带正电微粒(不计重力),发现此微粒恰能在两板间运动而不与板发生相互作用. 分析 (1)运用动能定理研究微粒在加速电场的过程.微粒进入半圆形金属板后,电场力提供向心力,列出等式求解.
(2)匀加速直线运动和匀速圆周运动运用各自的规律求解时间.
解答 解:(1)设微粒穿过AB小孔时的速度为v,根据动能定理,有qEd=$\frac{1}{2}$mv2-0…①
解得v=$\sqrt{\frac{2qEd}{m}}$
微粒进入半圆形金属板后,电场力提供向心力,有
qEAB=m$\frac{{v}^{2}}{L}$…②
联立①、②,得EAB=$\frac{2Ed}{R}$,
(2)从释放微粒开始,达到与O水平高度时水平位置最大,Lmax=d+L,
在电场E中加速度a=$\frac{Eq}{m}$,
运动时间t1=$\frac{v}{a}$=$\sqrt{\frac{2qEd}{m}}$$•\frac{m}{Eq}$=$\sqrt{\frac{2md}{qE}}$,
在AB轨道内运动路程为$\frac{1}{4}$×2πL=vt2
t2=$\frac{\frac{1}{2}πL}{v}$=$\frac{1}{2}πL$$\sqrt{\frac{m}{2qEd}}$,
总时间t=t1+t2=$\sqrt{\frac{2md}{qE}}$+$\frac{1}{2}πL$$\sqrt{\frac{m}{2qEd}}$
所以从释放微粒开始,经过(t1+t2)粒子第一次到达水平位置最大点.之后,经过t2达到AB板的上边,再经过t1达到与释放点在同一条竖直线上的点,然后返回;经过(t1+t2)第二次达到水平位置最大点.
从开始运动到第二次达到水平位置最大点的总时间:t=3(t1+t2)
同理,从开始运动到第三次达到水平位置最大点的总时间:t=5(t1+t2)
所以,从开始运动到第n次达到水平位置最大点的总时间:t=(2n-1)(t1+t2)=(2n-1)($\sqrt{\frac{2md}{qE}}$+$\frac{1}{2}πL$$\sqrt{\frac{m}{2qEd}}$);
答:(1)A、B之间电场的场强大小为$\frac{2Ed}{R}$.
(2)从释放微粒开始,经过(2n-1)($\sqrt{\frac{2md}{qE}}$+$\frac{1}{2}πL$$\sqrt{\frac{m}{2qEd}}$)时间微粒的水平位移最大,最大值为d+L.
点评 了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
圆周运动问题的解决析关键要通过受力分析找出向心力的来源.注意物体的往复运动.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,小明站在加速上升的电梯里,随电梯一起运动,在向上加速运动的过程中,下列说法正确的是( )
如图所示,小明站在加速上升的电梯里,随电梯一起运动,在向上加速运动的过程中,下列说法正确的是( )| A. | 小明所受的支持力与对电梯的压力是一对相互作用力 | |
| B. | 小明现在正处于失重状态 | |
| C. | 小明所受的重力和支持力是一对平衡力 | |
| D. | 小明所受的重力就是对电梯的压力 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 一斜面AB长为5m,倾角为30°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止释放,如图所示.斜面与物体间的动摩擦因数为$\frac{\sqrt{3}}{6}$,求
一斜面AB长为5m,倾角为30°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止释放,如图所示.斜面与物体间的动摩擦因数为$\frac{\sqrt{3}}{6}$,求查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. |  | B. | 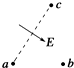 | C. | 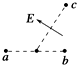 | D. | 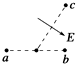 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
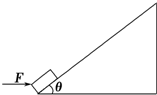 质量m=1kg的物体在F=20N的水平推力作用下,从足够长的粗糙斜面的底端A点由静止开始沿斜面运动,物体与斜面间动摩擦因数为μ=0.25,斜面固定不动,与水平地面的夹角θ=37°,力F作用4s后撤去,撤去力F后5s物体正好通过斜面上的B点.(已知sin 37°=0.6,cos 37°=0.8,g=10m/s2).求:
质量m=1kg的物体在F=20N的水平推力作用下,从足够长的粗糙斜面的底端A点由静止开始沿斜面运动,物体与斜面间动摩擦因数为μ=0.25,斜面固定不动,与水平地面的夹角θ=37°,力F作用4s后撤去,撤去力F后5s物体正好通过斜面上的B点.(已知sin 37°=0.6,cos 37°=0.8,g=10m/s2).求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 质量为m=20kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动.0~2.0s内F与运动方向相反,2.0~4.0s内F与运动方向相同,物体的速度一时间图象如图所示,已知g取10m/s2.求物体在前4秒内的位移多少?物体与水平面间的动摩擦数.
质量为m=20kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动.0~2.0s内F与运动方向相反,2.0~4.0s内F与运动方向相同,物体的速度一时间图象如图所示,已知g取10m/s2.求物体在前4秒内的位移多少?物体与水平面间的动摩擦数.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
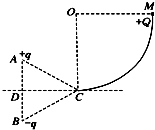 如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )
如图所示,竖直平面内$\frac{1}{4}$光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )| A. | 小球在圆弧轨道上运动过程机械能守恒 | |
| B. | C点电势与D点电势相同 | |
| C. | M点电势为$\frac{1}{2Q}$(mv02-2mgR) | |
| D. | 小球对轨道最低点C处的压力大小为mg+m$\frac{{{v}_{0}}^{2}}{R}$+k$\frac{Qq}{{L}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com