
第五章 平面向量
一.向量的相关概念
1.向量的定义: 叫做向量。
2.向量的模(长度):
①设  , 则
, 则 =
=
②若表示向量 的起点和终点的坐标分别为
的起点和终点的坐标分别为 ,则
,则
 =___________________
=___________________  =
=
3.零向量: 叫做零向量;
4.单位向量: 叫做单位向量;
5.共线(平行)向量: 叫做共线向量;
6.相等向量: 叫做相等向量;
7.相反向量: 叫做相反向量.
二. 向量的运算:
运 算
定义(法则)
坐标运算
加 法 运 算
减 法 运 算
实数与向量的积
平面向量的数量积
三3三三 .平面向量的基本定理:
1.如果向量 不共线,则同一平面内的任一向量
不共线,则同一平面内的任一向量 =____________________________,
=____________________________,
其中 称为________________
称为________________
2.向量 ______________
______________  _______________
_______________
其中 是沿
是沿 轴,
轴, 轴正向的单位向量。
轴正向的单位向量。
4.3.两个向量平行和垂直的充要条件: ,
,
①
 ;
;
② ∥
∥
 ;
;
③ 与
与 的夹角
的夹角 。
。
四.定比分点公式
1. 线段的定比分点定义
设点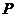 分向量
分向量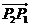 所成的定比为
所成的定比为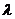 ,
,
①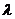 如何定义:
如何定义:
②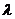 的符号如何确定:
的符号如何确定:
③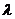 的大小如何确定:
的大小如何确定:
2.线段的定比分点坐标公式:
①设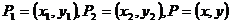 ,且
,且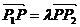 ,则
,则
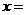 ______________
______________
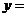 ________________
________________
②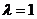 时,得中点坐标公式:
时,得中点坐标公式: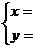
③点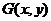 是
是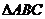 的重心,且
的重心,且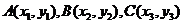 ,则
,则
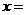 __________________
__________________ 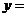 ___________________
___________________
五. 平移
1.点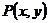 按
按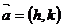 平移到
平移到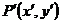 ,则
,则
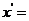 ________________
________________ 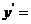 _________________
_________________
2.向量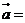
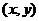 按向量
按向量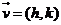 平移后的向量坐标是_____________
平移后的向量坐标是_____________
3.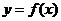 按向量
按向量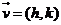 平移后得_____________________
平移后得_____________________
六. 解斜三角形
1.正弦定理:
= = 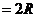 。
。
2.余弦定理:
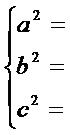
3.常用的三角形面积公式(至少写出三个)
4.已知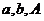 ,解三角形的各种情况
,解三角形的各种情况
若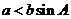 三角形_______
三角形_______
若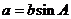 三角形_______
三角形_______
若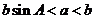 三角形_______
三角形_______
若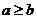 三角形_______
三角形_______
5.在三角形中常用的几个向量结论
①在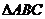 中,
中,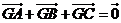
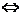 点
点 是
是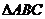 的___________
的___________
②在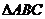 中,点
中,点 是
是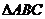 的垂心
的垂心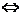 ___________________________________________
___________________________________________
③在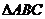 中,
中,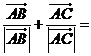 _____________________________
_____________________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com