精英家教网 >
试题搜索列表 >在利用蚕沙、人蓄粪便、秸秆、杂草、树叶等物质生产沼气的过程中，发挥作用的主要生物是什么
在利用蚕沙、人蓄粪便、秸秆、杂草、树叶等物质生产沼气的过程中，发挥作用的主要生物是什么答案解析
科目：czsx
来源：
题型：
有甲、乙两个工艺品加工厂，两个厂均有30名工人，两个工厂同时接到相同数量同种工艺品的订货单．甲工厂存该工艺品240件，乙工厂库存该工艺品300件，在此基础上，甲工厂完成订货任务还需要20天，乙工厂完成订货任务还需要25天．现在两个工厂同时生产该工艺品，生产5天时两工厂该工艺品总数量相同（设甲、乙两个加工厂工人全部参与生产，甲工厂每个工人每天的生产量相同．乙工厂每个工人每天的生产量相同）．
（1）求甲、乙两个加工厂每天各能加工多少件该种工艺品？
（2）若再两厂生产工艺品的过程中，又都同时接到与上次数量相同的该工艺品订货单，并且要求甲、乙两工厂完成这两次总订货量的时间均不超过55天．甲厂在完成第一次的订货量后，又生产了10天，为了使甲、乙两厂都能在规定的时间内完成这两次总订货量，甲厂派部分工人到乙厂帮助生产，则甲厂向乙厂有多少派人方案？
查看答案和解析>>
科目：czsx
来源：
题型：解答题
有甲、乙两个工艺品加工厂，两个厂均有30名工人，两个工厂同时接到相同数量同种工艺品的订货单．甲工厂存该工艺品240件，乙工厂库存该工艺品300件，在此基础上，甲工厂完成订货任务还需要20天，乙工厂完成订货任务还需要25天．现在两个工厂同时生产该工艺品，生产5天时两工厂该工艺品总数量相同（设甲、乙两个加工厂工人全部参与生产，甲工厂每个工人每天的生产量相同．乙工厂每个工人每天的生产量相同）．
（1）求甲、乙两个加工厂每天各能加工多少件该种工艺品？
（2）若再两厂生产工艺品的过程中，又都同时接到与上次数量相同的该工艺品订货单，并且要求甲、乙两工厂完成这两次总订货量的时间均不超过55天．甲厂在完成第一次的订货量后，又生产了10天，为了使甲、乙两厂都能在规定的时间内完成这两次总订货量，甲厂派部分工人到乙厂帮助生产，则甲厂向乙厂有多少派人方案？
查看答案和解析>>
科目：czsx
来源：不详
题型：解答题
有甲、乙两个工艺品加工厂，两个厂均有30名工人，两个工厂同时接到相同数量同种工艺品的订货单．甲工厂存该工艺品240件，乙工厂库存该工艺品300件，在此基础上，甲工厂完成订货任务还需要20天，乙工厂完成订货任务还需要25天．现在两个工厂同时生产该工艺品，生产5天时两工厂该工艺品总数量相同（设甲、乙两个加工厂工人全部参与生产，甲工厂每个工人每天的生产量相同．乙工厂每个工人每天的生产量相同）．
（1）求甲、乙两个加工厂每天各能加工多少件该种工艺品？
（2）若再两厂生产工艺品的过程中，又都同时接到与上次数量相同的该工艺品订货单，并且要求甲、乙两工厂完成这两次总订货量的时间均不超过55天．甲厂在完成第一次的订货量后，又生产了10天，为了使甲、乙两厂都能在规定的时间内完成这两次总订货量，甲厂派部分工人到乙厂帮助生产，则甲厂向乙厂有多少派人方案？
查看答案和解析>>
科目：czsx
来源：2009年黑龙江省（鹤、伊、双、绥）升学大考数学试卷（五）（解析版）
题型：解答题
有甲、乙两个工艺品加工厂，两个厂均有30名工人，两个工厂同时接到相同数量同种工艺品的订货单．甲工厂存该工艺品240件，乙工厂库存该工艺品300件，在此基础上，甲工厂完成订货任务还需要20天，乙工厂完成订货任务还需要25天．现在两个工厂同时生产该工艺品，生产5天时两工厂该工艺品总数量相同（设甲、乙两个加工厂工人全部参与生产，甲工厂每个工人每天的生产量相同．乙工厂每个工人每天的生产量相同）．
（1）求甲、乙两个加工厂每天各能加工多少件该种工艺品？
（2）若再两厂生产工艺品的过程中，又都同时接到与上次数量相同的该工艺品订货单，并且要求甲、乙两工厂完成这两次总订货量的时间均不超过55天．甲厂在完成第一次的订货量后，又生产了10天，为了使甲、乙两厂都能在规定的时间内完成这两次总订货量，甲厂派部分工人到乙厂帮助生产，则甲厂向乙厂有多少派人方案？
查看答案和解析>>
科目：czsx
来源：
题型：
（2010•金东区模拟）如图，线段AB的端点在边长为1的小正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°．得到线段AC．
（1）若将此网格放在一平面直角坐标系中，已知点A（1，3），点B（-2，-1〕，直接写出点C的坐标
（2）线段AB在旋转到线段AC的过程中，求线段AB扫过的区域的面积；
（3）若利用（2）中得到的区域纸片，将它围成一个几何体的侧面，求该几何体底面圆的半径长．
查看答案和解析>>
科目：czsx
来源：
题型：
在抗击“SARS”的过程中，某厂甲、乙两工人按上级指示同时做一批等数量的防护服．开始时，乙比甲每天少做3件，到甲、乙两人都剩下80件时，乙比甲多做了2天，这时，甲保持工作效率不变，乙提高了工作效率后比原来每天多做5件，这样甲、乙两人同时完成了任务．求甲、乙两人原来每天各做多少件防护服？
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
先阅读再化简求值：
（1）在化简
的过程中．小张和小李的化简结果不一样：小张的化简过程如下：
原式=
===-小李的化简过程如下：
原式=
===-请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由？
（2）请你利用上面所学的方法，化简求值：已知
x=，求x
2+2x-3的值．
查看答案和解析>>
科目：czsx
来源：
题型：
8、在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
阅读材料：为解方程（x
2-1）
2-5（x
2-1）+4=0，我们可以将x
2-1看作一个整体，然后设x
2-1=y…①，
那么原方程可化为y
2-5y+4=0，
解得y
1=1，y
2=4．
当y=1时，x
2-1=1，∴x
2=2，∴x=±
；
当y=4时，x
2-1=4，∴x
2=5，∴x=±
，
故原方程的解为x
1=
，x
2=
-，x
3=
，x
4=
-．
解答问题：
（1）上述解题过程，在由原方程得到方程①的过程中，利用
法达到了解方程的目的，体现了转化的数学思想；
（2）请利用以上知识解方程x
4-x
2-6=0．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
阅读材料：
为解方程（x-1）
2-5（x-1）+4=0时，我们可以将x-1看作一个整体，然后设x-1=y…．①，那么原方程可化为y
2-5y+4=0，解得y
1=1，y
2=4．当y=1时，x-1=1，∴x=2；当y=4时，x-1=4，∴x=5；故原方程的解为x
1=2，x
2=5．
解答问题：
（1）上述解题过程，在由原方程得到方程①的过程中，运用了
换元
换元
法达到了解方程的目的，体现了转化的数学思想；
（2）请利用以上知识解方程：（3x+5）
2-4（3x+5）+3=0．
查看答案和解析>>
科目：czsx
来源：
题型：
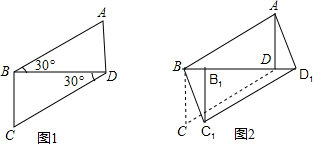
活用知识，解决问题．
（1）轮船顺水航行40千米所需时间和逆水航行30千米所需时间相等，已知水流速度为3千米/小时，求轮船在静水中的速度．
（2）将两块全等的含30°角的三角尺如图（1）摆放在一起，设较短的直角边为1
①四边形ABCD是平行四边形吗？说出你的结论和理由
；
②将Rt△BCD沿射线BD方向平移到Rt△B
1C
1D③位置，四边形ABC
1D
1是平行边边形吗？说明你的结论和理由
；
③在Rt△BCD沿射线BD方向平移的过程中，当B的移动距离为
四边形ABC
1D
1为矩形，其理由是
．
（3）阅读理解：
解方程x
4-3x
2+2=0，设x
2=y，则原方程可分为y
2-3y+2=0，解得：y
1=2，y
2=1．
（1）当y=2时，x
2=2，解得x=±
；
（2）当y=1时，x
2=1，解题x=±1，故原方程的解是：x
1=
，x
2=-
，x
3=1，x
4=-1，请利用以上方法解方程：（x
2-2x）
2-2x
2+4x-3=0．
查看答案和解析>>
科目：czsx
来源：
题型：
为了解某中学八年级250名学生的数学成绩，从中抽取了50名学生的数学成绩进行分析，得到下表：
| 分数 |
60分以下 |
60.5～70.5分 |
70.5分～80.5分 |
80.5分～90.5分 |
90.5分～100.5分 |
合计 |
| 频数 |
3 |
6 |
b |
17 |
15 |
50 |
| 频率 |
a |
0.12 |
0.18 |
0.34 |
0.3 |
1 |
（1）在这次抽样分析的过程中，样本是
；
（2）表中的数据a=
，b=
；
（3）估计该校八年级这次考试的数学平均成绩约为
分；
（4）在这次考试中该校八年级数学成绩在90.5～100.5范围内的人数为
人．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如，求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
，即1+2+3+4+…+n=
．
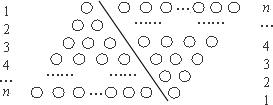
（1）仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
查看答案和解析>>
科目：czsx
来源：
题型：
31、某铁路施工队在建设铁路的过程中，需要打通一座小山（如图），设计时要测量隧道AB的长度，恰好在山的前面有一片空地，测量人员想借助于这个有利的地形，利用三角形全等的知识测量出需要开挖的隧道长度，请你帮助测量人员设计测量方法，画出图形，并说明理由．（要求：至少两种方法）
查看答案和解析>>
科目：czsx
来源：
题型：
（2002•淮安）（1）计算：
(1+)÷（2）解不等式组
，并把它的解集在数轴上表示出来．
（3）解方程：
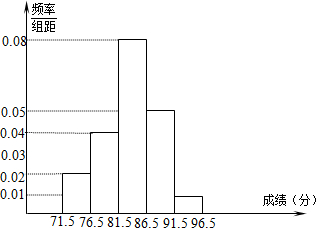
()2+6=5()（4）为了了解某校初三年级200名学生的数学毕业考试成绩，从中抽取了20名学生的数学成绩进行分析，下面是根据这20名学生的数学成绩画出的频率分布直方图，根据题中给出的条件回答下列问题：
①在这次抽样分析的过程中，样本容量是
20
20
②71.5-76.5（分）这一小组的频率是
0.1
0.1
；
③在这次毕业考试中，该校初三年级200名学生的数学成绩在86.5-96.5（分）这个范围内的人数约为
60
60
人．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
先阅读，再化简求值：
（1）在化简
的过程中．小张和小李的化简结果不一样：
小张的化简过程如下：
原式=
===-小李的化简过程如下：
原式=
===-请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由？
（2）请你利用上面所学的方法，化简求值：已知
x=，求
(+)×的值．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，在猫捉老鼠的过程中，老鼠沿着长方形的两边A→B→D的路线逃窜，猫同时沿着楼梯A→C→D去追捕，结果猫在D点捉住了老鼠，线段CD长0.6米．
（1）设楼梯A→C的总长为x米，猫捉老鼠所用的时间为t秒．请完成右边的表格；
| 楼梯A-C的总长为 |
x米 |
| AB+BC的长为 |
|
| 猫追捕的路程为 |
|
| 老鼠逃窜的路程为 |
|
| 设猫捉老鼠所用的时间为 |
t秒 |
| 猫的速度是 |
|
| 老鼠的速度是 |
|
（2）已知老鼠的速度是猫速度的
．你能不能利用“速度”这一条件将有关的代数式连接起来？
查看答案和解析>>
科目：czsx
来源：
题型：
为解方程（x
2-1）
2-5（x
2-1）+4=0，我们可以将x
2-1视为一个整体，然后设x
2-1=y，则
（x
2-1）2=y
2，原方程化为y
2-5y+4=0．①
解得y
1=1，y
2=4
当y=1时，x
2-1=1．∴x
2=2．∴x=±
；
当y=4时，x
2-1=4，∴x
2=5，∴x=±
．
∴原方程的解为x
1=
，x
2=-
，x
3=
，x
4=-
解答问题：
（1）填空：在由原方程得到方程①的过程中，利用
换元
换元
法达到了降次的目的，体现了
转化
转化
的数学思想．
（2）解方程：x
4-x
2-6=0．
查看答案和解析>>
科目：czsx
来源：
题型：
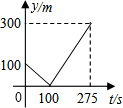
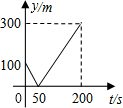
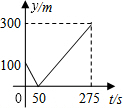
甲、乙两个准备在一段长为1200米的笔直公路上进行跑步，甲、乙跑步的速度分别为4m/s和6m/s，起跑前乙在起点，甲在乙前面100米处，若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲、乙两之间的距离y（m）与时间t（s）的函数图象是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
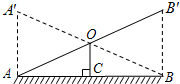
（2012•广西模拟）你一定玩过跷跷板吧！如图是小明和小刚玩跷跷板的示意图，横板绕它的中点O上下转动，立柱OC与地面垂直．当一方着地时，另一方上升到最高点．
（1）在上下转动横板的过程中，两人上升的最大高度AA′，BB′有何数量关系？为什么？
（2）若立柱OC的高为0.5米，求上升最大高度AA′的值．
查看答案和解析>>
