
科目:gzsx 来源: 题型:
(本小题满分13分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G![]() 点,E点在AB上,平面PEC⊥平面PDC.
点,E点在AB上,平面PEC⊥平面PDC.
(Ⅰ)求证:AG∥平面PEC;
(Ⅱ)求AE的长;
(Ⅲ)求二面角E—PC—A的正弦值.
 |
科目:gzsx 来源: 题型:
 (本小题满分13分)如图,在四棱锥P —ABCD中,底面ABCD是一直角梯形,∠BAD = 90°,AD∥BC,AB=BC=1,AD=2.且PA⊥底面ABCD,PD与底面ABCD成30°角,AE⊥PD于E,
(本小题满分13分)如图,在四棱锥P —ABCD中,底面ABCD是一直角梯形,∠BAD = 90°,AD∥BC,AB=BC=1,AD=2.且PA⊥底面ABCD,PD与底面ABCD成30°角,AE⊥PD于E,
(Ⅰ)求证:面PCD⊥面ABE;
(Ⅱ)求异面直线AE与CD所成角的余弦值.
科目:gzsx 来源: 题型:
(本小题满分13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4, G为PD中点,E点在AB上,平面PEC⊥平面PDC.
(Ⅰ)求证:AG⊥平面PCD;
(Ⅱ)求证:AG∥平面PEC;
(Ⅲ)求点G到平面PEC的距离.
 |
科目:gzsx 来源: 题型:
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.

科目:gzsx 来源:2013届北京师大附中高二上学期期中考试数学 题型:解答题
(本小题满分13分)
如图,在四棱锥 -
- 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 、
、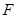 分别为
分别为 、
、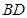 的中点,侧面
的中点,侧面 底面
底面 ,且
,且 。
。
(Ⅰ)求证: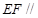 平面
平面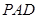 ;
;
(Ⅱ)求证:平面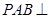 平面
平面 ;
;
(Ⅲ)求三棱锥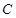 -
-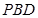 的体积。
的体积。
科目:gzsx 来源:2010-2011学年江苏省高三学情调研考试数学卷 题型:解答题
(本小题满分14分)
如图,在四棱锥P—ABCD中,AB∥CD,CD=2AB,AB 平面PAD,E为PC的中点.
平面PAD,E为PC的中点.
(1)求证:BE∥平面PAD;
(2)若AD PB,求证:PA
PB,求证:PA 平面ABC D.
平面ABC D.

科目:gzsx 来源:2014届山东省莱芜市高二上学期期末考试文数试卷(解析版) 题型:解答题
(本小题满分13分)
如图,在四棱锥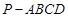 中,底面
中,底面 是正方形.已知
是正方形.已知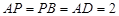 ,
, .
.

(Ⅰ)求证: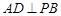 ;
;
(Ⅱ)求四棱锥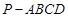 的体积
的体积 .
.
科目:gzsx 来源:2010-2011学年浙江省高三上学期期中考试数学文卷 题型:解答题
本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC= .
.
(Ⅰ)证明:CD⊥平面PAC;
(Ⅱ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.

科目:gzsx 来源:2011-2012学年浙江省三校高三联考理科数学 题型:解答题
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD= .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,
试确定t的值

科目:gzsx 来源:北京市宣武区2010年高三第一次质量检测数学(理)试题 题型:解答题
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°, 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.

科目:gzsx 来源: 题型:
(本小题满分14分) 如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
|

|
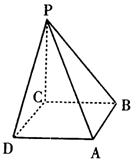
(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且![]() ,
,![]() ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.

科目:gzsx 来源: 题型:
(08年安徽信息交流文)(本小题满分14分) 如图,在四棱锥P-ABCD中,PB⊥底面
如图,在四棱锥P-ABCD中,PB⊥底面![]() ,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
(1)求二面角P-CD-B的正切值;
(2)求异面直线PA与CD所成的角;
(3)求证:PC∥平面EBD。
科目:gzsx 来源:北京市宣武区2010年高三第一次质量检测数学(文)试题 题型:解答题
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.
科目:gzsx 来源:2010-2011学年江苏省盐城市高三摸底考试数学卷 题型:解答题
(本小题满分14分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA⊥PD,E、F分别为PC、BD的中点。
(I)求证:直线EF//平面PAD;
(II)求证:直线EF⊥平面PDC。

科目:gzsx 来源: 题型:
(本小题满分14分)
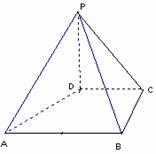 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
求证:PC⊥BC;
求点A到平面PBC的距离。
科目:gzsx 来源:2010-2011学年江苏省高三预测卷3数学 题型:解答题
(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD= ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.

(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
科目:gzsx 来源:2010-2011学年广东省高三综合测试数学文卷 题型:解答题
(本小题满分14分)
如图,在四棱锥P-ABCD中,PD上⊥平面ABCD,AD⊥CD,且BD平分∠ADC,
 E为PC的中点,AD=CD=l,BC=PC,
E为PC的中点,AD=CD=l,BC=PC,
(Ⅰ)证明PA∥平面BDE;
(Ⅱ)证明AC⊥平面PBD:
(Ⅲ)求四棱锥P-ABCD的体积,
科目:gzsx 来源: 题型:
(08年安徽信息交流) (本小题满分14分)如图,在四棱锥P-ABCD中,PB⊥底面![]() ,CD⊥PD,底面ABCD为直角
,CD⊥PD,底面ABCD为直角 梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A-BE-D的大小。
科目:gzsx 来源: 题型:
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,![]() 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.
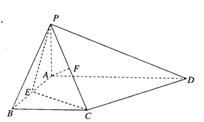
科目:gzsx 来源:北京市宣武区2010年高三第一次质量检测数学(文)试题 题型:解答题
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.
