科目：gzsx 来源：2013年浙江省六校联考理数 题型：022

在Rt△ABC中，AC＝2，BC＝2，已知点P是△ABC内一点，则·(＋)的最小值是________．

查看答案和解析>>

科目：gzsx 来源：浙江省宁波市鄞州区2012届高三高考适应性考试(3月)数学理科试题 题型：013

在Rt△ABC中，AC＝2，BC＝2，已知点P是△ABC内一点，则·(＋)的最小值是

[　　]

A．－2

B．－1

C．0

D．1

查看答案和解析>>

科目：gzsx 来源： 题型：

在Rt△ABC中，AC=2，BC=2，已知点P是△ABC内一点，则

PC

•(

PA

+

PB

)的最小值是（　　）

A．-2

B．-1

C．0

D．1

查看答案和解析>>

科目：gzsx 来源： 题型：

（2013•浙江模拟）在Rt△ABC中，AC=2，BC=2，已知点P是△ABC内一点，则

PC

•(

PA

+

PB

)的最小值是

-1

．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年浙江省一级重点中学（六校）高三第一次联考数学试卷（理科）（解析版） 题型：填空题

在Rt△ABC中，AC=2，BC=2，已知点P是△ABC内一点，则

的最小值是．

查看答案和解析>>

科目：gzsx 来源：2012年浙江省宁波市鄞州区高三3月适应性考试数学试卷（理科）（解析版） 题型：选择题

在Rt△ABC中，AC=2，BC=2，已知点P是△ABC内一点，则

的最小值是（）
A．-2
B．-1
C．0
D．1

查看答案和解析>>

科目：gzsx 来源：浙江省模拟题 题型：单选题

在Rt △ABC中，AC=2 ，BC=2 ，已知点P是△ABC内一点，则

的最小值是

[ ]

A、-2
B、-1
C、0
D、1

查看答案和解析>>

科目：gzsx 来源： 题型：

（2012•杨浦区一模）已知△ABC的三个顶点在抛物线Γ：x²=y上运动．
（1）求Γ的准线方程；
（2）已知点P的坐标为（2，6），F为抛物线Γ的焦点，求|AP|+|AF|的最小值，并求此时A点的坐标；
（3）若点A在坐标原点，BC边过定点N（0，1），点M在BC上，且

AM

•

BC

=0，求点M的轨迹方程．

查看答案和解析>>

科目：gzsx 来源：2012年上海市杨浦区高考数学一模试卷（文科）（解析版） 题型：解答题

已知△ABC的三个顶点在抛物线

：x²=y上运动．
（1）求

的准线方程；
（2）已知点P的坐标为（2，6），F为抛物线

的焦点，求|AP|+|AF|的最小值，并求此时A点的坐标；
（3）若点A在坐标原点，BC边过定点N（0，1），点M在BC上，且

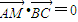，求点M的轨迹方程．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的焦点和上顶点分别为F₁、F₂、B，我们称△F₁BF₂为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似三角形，则称这两个椭圆为“相似椭圆”，且特征三角形的相似比即为相似椭圆的相似比．已知椭圆C₁

x2

a2

+

y2

b2

=1以抛物线y2=4

3

x的焦点为一个焦点，且椭圆上任意一点到两焦点的距离之和为4．（1）若椭圆C₂与椭圆C₁相似，且相似比为2，求椭圆C₂的方程．
（2）已知点P（m，n）（mn≠0）是椭圆C₁上的任一点，若点Q是直线y=nx与抛物线x2=

1

mn

y异于原点的交点，证明点Q一定落在双曲线4x²-4y²=1上．
（3）已知直线l：y=x+1，与椭圆C₁相似且短半轴长为b的椭圆为C_b，是否存在正方形ABCD，使得A，C在直线l上，B，D在曲线C_b上，若存在求出函数f（b）=S_ABCD的解析式及定义域，若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知圆C的圆心在坐标原点，且过点M（1 ，

3

）．
（1）求圆C的方程；
（2）已知点P是圆C上的动点，试求点P到直线x+y-4=0的距离的最小值；
（3）若直线l与圆C相切，且l与x，y轴的正半轴分别相交于A，B两点，求△ABC的面积最小时直线
l的方程．

查看答案和解析>>

科目：gzsx 来源：2010年湖南省长沙一中学业水平考试数学模拟试卷（三）（解析版） 题型：解答题

已知圆C的圆心在坐标原点，且过点M（

）．
（1）求圆C的方程；
（2）已知点P是圆C上的动点，试求点P到直线x+y-4=0的距离的最小值；
（3）若直线l与圆C相切，且l与x，y轴的正半轴分别相交于A，B两点，求△ABC的面积最小时直线
l的方程．

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

已知圆C的圆心在坐标原点，且过点M（ $数学公式$ ）．
（1）求圆C的方程；
（2）已知点P是圆C上的动点，试求点P到直线x+y-4=0的距离的最小值；
（3）若直线l与圆C相切，且l与x，y轴的正半轴分别相交于A，B两点，求△ABC的面积最小时直线
l的方程．

查看答案和解析>>

科目：gzsx 来源： 题型：

如图2-2-10,已知点P为△ABC所在平面外任一点,点D,E,F分别在射线PA,PB,PC上,并且.

图2-2-10

求证:平面DEF∥平面ABC.

查看答案和解析>>

科目：gzsx 来源：2010年五校联合教学调研数学试卷（理科）（解析版） 题型：解答题

已知椭圆C：

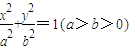的焦点和上顶点分别为F₁、F₂、B，我们称△F₁BF₂为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似三角形，则称这两个椭圆为“相似椭圆”，且特征三角形的相似比即为相似椭圆的相似比．已知椭圆C₁

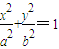以抛物线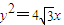

的焦点为一个焦点，且椭圆上任意一点到两焦点的距离之和为4．（1）若椭圆C₂与椭圆C₁相似，且相似比为2，求椭圆C₂的方程．
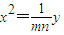（2）已知点P（m，n）（mn≠0）是椭圆C₁上的任一点，若点Q是直线y=nx与抛物线

异于原点的交点，证明点Q一定落在双曲线4x²-4y²=1上．
（3）已知直线l：y=x+1，与椭圆C₁相似且短半轴长为b的椭圆为C_b，是否存在正方形ABCD，使得A，C在直线l上，B，D在曲线C_b上，若存在求出函数f（b）=S_ABCD的解析式及定义域，若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源：安徽省模拟题 题型：解答题

如图，在平面直角坐标系xOy中，椭圆C：

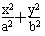＝1（a＞b＞0）的离心率为

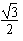，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x－y＋2＝0相切，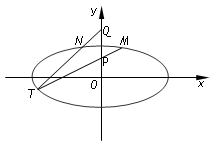
（1）求椭圆C的方程；
（2）已知点P（0，1），Q（0，2），设M，N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上。

查看答案和解析>>

科目：gzsx 来源： 题型：

（2013•南京二模）在平面直角坐标系xOy中，椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)过点A(

a

2

，

a

2

)，B(

3

，1)．
（1）求椭圆C的方程；
（2）已知点P（x₀，y₀）在椭圆C上，F为椭圆的左焦点，直线l的方程为x₀x+3y₀y-6=0．
①求证：直线l与椭圆C有唯一的公共点；
②若点F关于直线l的对称点为Q，求证：当点P在椭圆C上运动时，直线PQ恒过定点，并求出此定点的坐标．

查看答案和解析>>

科目：gzsx 来源： 题型：

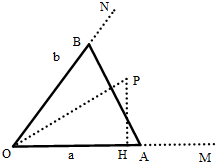（2013•镇江二模）如图所示，有两条道路OM与ON，∠MON=60°，现要铺设三条下水管道OA，OB，AB（其中A，B分别在OM，ON上），若下水管道的总长度为3km，设OA=a（km），OB=b（km）．
（1）求b关于a的函数表达式，并指出a的取值范围；
（2）已知点P处有一个污水总管的接口，点P到OM的距离PH为

3

4

km，到点O的距离PO为

7

4

km，问下水管道AB能否经过污水总管的接口点P？若能，求出a的值，若不能，请说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

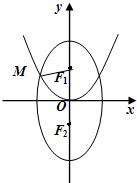与向量、圆交汇．例5：已知F₁、F₂分别为椭圆C₁：

y2

a2

+

x2

b2

=1(a＞b＞0)的上、下焦点，其中F₁也是抛物线C₂：x²=4y的焦点，点M是C₁与C₂在第二象限的交点，且|MF1|=

5

3

．
（1）求椭圆C₁的方程；
（2）已知点P（1，3）和圆O：x²+y²=b²，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：

AP

=-λ

PB

，

AQ

=λ

QB

，（λ≠0且λ≠±1）．问点Q是否总在某一定直线上？若在，求出这条直线，否则，说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

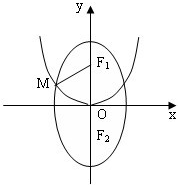如图，已知F₁、F₂分别为椭圆C1：

y2

a2

+

x2

b2

=1(a＞b＞0)的上、下焦点，其中F₁也是抛物线C2：x2=4y的焦点，点M是C₁与C₂在第二象限的交点，且|MF1|=

5

3

．
（1）求椭圆C₁的方程；
（2）已知点P（1，3）和圆O：x²+y²=b²，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：

AP

=-λ

PB

，

AQ

=λ

QB

（λ≠0且λ≠±1），
求证：点Q总在某条定直线上．

查看答案和解析>>

练习册

高中

初中

小学

在rt三角形abc，ac＝bc＝2，已知点p答案解析