练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知矩阵M=4，-1,2，-1，向量α=7,5

    已知矩阵M=4，-1,2，-1，向量α=7,5答案解析

    科目：gzsx 来源： 题型：

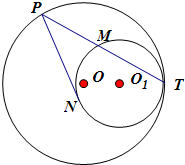    （2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
    若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
    B．选修4-2：矩阵与变换
    已知矩阵M=
    21
    34

    （1）求矩阵M的逆矩阵；
    （2）求矩阵M的特征值及特征向量；
    C．选修4-2：矩阵与变换
    在平面直角坐标系x0y中，求圆C的参数方程为
    x=-1+rcosθ
    y=rsinθ
    (θ    为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
    π
    4
    )=2
    		2
    ．若直线l与圆C相切，求r的值．
    D．选修4-5：不等式选讲
    已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：1＜a+b＜
    4
    3
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知矩阵M有特征值1=4及对应的一个特征向量e1=，并有特征值2=-1及对应的一个特征向量e2=.

    （1）求矩阵M；（2）求M2 008e2.

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年江苏省泰州市姜堰市高三（下）期初数学试卷（解析版） 题型：解答题

    已知矩阵M=有特征值λ1=4及对应的一个特征向量．
    （1）求矩阵M；
    （2）求曲线5x2+8xy+4y2=1在M的作用下的新曲线方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    选做题（选修4—2：矩阵与变换）已知矩阵M有特征值λ1=4及对应的一个特征向量e1=，并有特征值λ2=-1及对应的一个特征向量e2=.

    (1)求矩阵M；

    (2)求M2 008e2.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知矩阵M有特征值λ1=8及对应的一个特征向量e1=
    1
    1
    ，并有特征值λ2=2及对应的一个特征向量e2=
    1
    -2
    ，则矩阵M=
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    [选做题]在下面A，B，C，D四个小题中只能选做两题，每小题10分，共20分．
    A．选修4-1：几何证明选讲
    如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC到点D，使CD=AC，连接AD交⊙O于点E，连接BE与AC交于点F，判断BE是否平分∠ABC，并说明理由．
    B．选修4-2：短阵与变换
    已知矩阵M=
    1
    2
    		0
    02
    ，矩阵M对应的变换把曲线y=sinx变为曲线C，求C的方程．
    C．选修4-4：坐标系与参数方程
    已知曲线C的极坐标方程是ρ=4sin(θ+
    π
    4
    )    ，求曲线C的普通方程．
    D．选修4-5：不等式选讲
    已知x，y，z∈R，且x+y+z=3，求x2+y2+z2的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•盐城三模）选修4-2：矩阵与变换
    已知矩阵M=
    .
    1a
    b1
    .
    对应的变换将点A（1，1）变为A′（0，2），将曲线C：xy=1变为曲线C′．
    （1）求实数a，b的值；
    （2）求曲线C′的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•南京一模）选修4-2：矩阵与变换
    已知矩阵M=
    01
    10
    ，N=
    0-1
    10
    ．在平面直角坐标系中，设直线2x-y+1=0在矩阵MN对应的变换作用下得到曲线F，求曲线F的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•泉州模拟）选修4-2：矩阵与变换
    已知矩阵M=
    a2
    -13
    的一个特征值为1．
    （Ⅰ）求矩阵M的另一个特征值；
    （Ⅱ）设α=
    3
    2
    ，求M5α．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    选修4-2：矩阵与变换
    已知矩阵M=
    a    1
    c    0
    的一个特征值为-l，属于它的一个特征向量e1=
      1
    -3
    ．
    （1）求矩阵M；
    （2）若点P（1，1）经过矩阵M所对应的变换得到点Q，求点Q的坐标．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    选修4-2：矩阵与变换
    已知矩阵M=
    1    x
    2    1
    的一个特征值为-1，求其另一个特征值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知矩阵M=
    1b
    c2
    有特征值λ1=4及对应的一个特征向量
    e1
    =
    2′
    3′
    ．
    （1）求矩阵M；
    （2）求曲线5x2+8xy+4y2=1在M的作用下的新曲线方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （1）选修4-2：矩阵与变换
    已知矩阵M=
    01
    10
    ，N=
    0-1
    10

    （Ⅰ）求矩阵NN；
    （Ⅱ）若点P（0，1）在矩阵M对应的线性变换下得到点P′，求P′的坐标．
    （2）选修4-4：坐标系与参数方程
    在直角坐标系xOy中，直线l的参数方程是
    x=t
    y=2t+1
    （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程是ρ=2cosθ（Ⅰ）在直角坐标系xOy中，求圆C的直角坐标方程
    （Ⅱ）求圆心C到直线l的距离．
    （3）选修4-5：不等式选讲
    已知函数f（x）=|x-1|
    （Ⅰ）解不等式f（x）＞2；
    （Ⅱ）求函数y=f（-x）+f（x+5）的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    [选修4-2：矩阵与变换]
    已知矩阵M=
    1
    c
    b
    2
    有特征值λ1=4及对应的一个特征向量
    e1
    =
    2
    3
    ，求曲线5x2+8xy+4y2=1在M的作用下的新曲线方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （1）选修4-2：矩阵与变换
    已知矩阵M=
    7-6
    4-3
    ，向量
    ξ 
    =
    6
    5
    ．
    （I）求矩阵M的特征值λ1、λ2和特征向量
    ξ
    1    和
    ξ2
    ；
    （II）求M6
    ξ
    的值．
    （2）选修4-4：坐标系与参数方程
    在平面直角坐标系xOy中，已知曲线C的参数方程为
    x=2cosα
    y=sinα
    (α为参数)    ．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ-
    π
    4
    )=2
    		2
    ．
    （Ⅰ）求直线l的直角坐标方程；
    （Ⅱ）点P为曲线C上的动点，求点P到直线l距离的最大值．
    （3）选修4-5：不等式选讲
    （Ⅰ）已知：a、b、c∈R+，求证：a2+b2+c2≥
    1
    3
    (a+b+c)2    ；    
    （Ⅱ）某长方体从一个顶点出发的三条棱长之和等于3，求其对角线长的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知矩阵M=
    2a
    bc
    ，其中a，b，c∈R，若点P（1，-2）在矩阵M的变换下得到点Q（-4，0），且属于特征值-1的一个特征向量是
    1
    -1
    ，求a，b，c之值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知矩阵M=
    2a
    21
    ，其中a∈R，点P（1，-2）在矩阵M的变换下得到点P′（-4，0），则实数a=
    3
    3
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （1）已知矩阵M=
    2a
    21
    ，其中a∈R，若点P（1，-2）在矩阵M的变换下得到点P'（-4，0）
    （i）求实数a的值；
    （ii）求矩阵M的特征值及其对应的特征向量．
    （2）在平面直角坐标系xOy中，动圆x2+y2-8xcosθ-6ysinθ+7cos2θ+8=0（a∈R）的圆心为P（x0，y0），求2x0-y0的取值范围．
    （3）已知a，b，c为实数，且a+b+c+2-2m=0，a2+
    1
    4
    b2+
    1
    9
    c2    +m-1=0．
    ①求证：a2+
    1
    4
    b2+
    1
    9
    c2≥
    (a+b+c)2
    14
    ；
    ②求实数m的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网A、选修4-1：几何证明选讲 
    如图，PA与⊙O相切于点A，D为PA的中点，
    过点D引割线交⊙O于B，C两点，求证：∠DPB=∠DCP．
    B．选修4-2：矩阵与变换
    已知矩阵M=
    12
    2x
    的一个特征值为3，求另一个特征值及其对应的一个特征向量．
    C．选修4-4：坐标系与参数方程
    在极坐标系中，圆C的方程为ρ=2
    		2
    sin(θ+
    π
    4
    )    ，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=t
    y=1+2t
    （t为参数），判断直线l和圆C的位置关系．
    D．选修4-5：不等式选讲
    求函数y=
    		1-x
    +
    		4+2x
    的最大值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

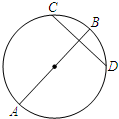    （2013•宿迁一模）【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，已知AB，CD是圆O的两条弦，且AB是线段CD的 垂直平分线，若AB=6，CD=2
    		5
    ，求线段AC的长度．
    B．选修4-2：矩阵与变换（本小题满分10分）
    已知矩阵M=
    21
    1a
    的一个特征值是3，求直线x-2y-3=0在M作用下的新直线方程．
    C．选修4-4：坐标系与参数方程（本小题满分10分）
    在平面直角坐标系xOy中，已知曲线C的参数方程是
    x=cosα
    y=sinα+1
    （α是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程．
    D．选修4-5：不等式选讲（本小题满分10分）
    已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R，求正实数a的取值范围．

    查看答案和解析>>